题目内容

如果复数z=3+ai满足条件|z-2|＜2，那么实数a的取值范围为
 
．
考点：复数求模
专题：数系的扩充和复数
分析：由模长公式和已知条件可得a的不等式，解不等式可得．
解答： 解：∵z=3+ai满足条件|z-2|＜2，
∴|1+ai|＜2，即
12+a2
＜2，
平方可得a2＜3，解得-
3
＜a＜
3
，
∴实数a的取值范围为（-
3
，
3
），
故答案为：（-
3
，
3
）
点评：本题考查复数的模长公式，涉及不等式的解法，属基础题．
练习册系列答案
相关题目
已知0＜β＜
π
4
＜α＜
π
2
，cos（2α-β）=-
11
14
，sin（α-2β）=
4
3
7
，求sin
α+β
2
的值．
在平面直角坐标系x0y中，直线
x=a-t
y=t
（t为参数）与圆
x=1+cosθ
y=sinθ
（θ为参数）相切，切点在第一象限，则实数a的值为
 
．
已知（4
4
1
x
+
3x2
）n展开式中的倒数第三项的二项式系数为45，则n=
 
．
圆C的极坐标方程为ρ=2cos（θ+
π
4
），直线l的参数方程为
x=
2
t
y=
2
t+4
2
（其中t为参数），过直线l上的点P向圆C引切线，切点为A，则切线长PA的最小值是
 
．
在平面直角坐标系xoy中，直线l的参数方程为
x=t+2
y=2-t
（参数t∈R），圆C的参数方程为
x=2cosθ
y=2sinθ+2
（参数θ∈[0，2π）），直线l交圆C于A、B两点，则|AB|=
 
．
已知复数z=
4+3i
(1-2i)2
，则|z|=
 
．
阅读下题的解题方法：
例题：已知x＞0，y＞0，且x+y=1，求
1
x
+
2
y
的最小值．
解：
1
x
+
2
y
=（x+y）（
1
x
+
2
y
）=1+
2x
y
+
y
x
+2≥3+2
2x
y
•
y
x
=3+2
2
，当且仅当
2x
y
=
y
x
x+y=1.
时，即
x=
2
-1
y=2-
2
.
时，取等号．∴当
x=
2
-1
y=2-
2
.
时，
1
x
+
2
y
取最小值，其最小值为3+2
2
．
类比上述解题方法，可求得函数f（x）=
4
x
+
9
1-2x
，x∈（0，
1
2
）的最小值为
 
．
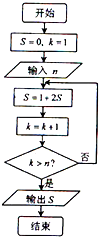阅读如图所示的程序框图，运行相应的程序，如果输入某个正整数n后，输出的S∈（30，40），那么n的值为（　　）
A、3B、4C、5D、6

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网