题目内容
10.已知f(x)=(m2-m-1)x-5m-1是幂函数,且在区间(0,+∞)上单调递增.(Ⅰ)求m的值;
(Ⅱ)解不等式f(x-2)>16.
分析 (Ⅰ)根据幂函数的定义以及函数的单调性求出m的值即可;(Ⅱ)问题转化为(x-2)4>24,求出不等式的解集即可.
解答 解:(Ⅰ)∵f(x)=(m2-m-1)x-5m-1是幂函数,
∴m2-m-1=1,解得:m=-1或m=2,
m=-1时,f(x)=x4,m=2时,f(x)=x-11,
若f(x)在区间(0,+∞)上单调递增,
则m=-1;
(Ⅱ)由(Ⅰ)得:f(x)=x4,
由f(x-2)>16,
得:(x-2)4>24,
故|x-2|>2,解得:x>4或x<0,
点评 本题考查了函数的单调性、最值问题,考查幂函数的定义,是一道基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.以x轴为对称轴,以原点为顶点且过圆x2+y2-2x+6y+9=0的圆心的抛物线的方程是( )
| A. | y=3x2或y=-3x2 | B. | y=3x2 | C. | y2=-9x或y=3x2 | D. | y2=9x |
2.在等差数列{an}中,Sn是该数列的前n项和,已知a4+a8=4,则S11+a6=( )
| A. | 12 | B. | 16 | C. | 24 | D. | 48 |
20.空气质量指数(AirQualityIndex,简称AQI)是定量描述空气质量状况的指数.AQI数值越小,说明空气质量越好.某地区1月份平均AQI(y)与年份(x)具有线性相关关系.下列最近3年的数据:
根据数据求得y关于x的线性回归方程为$\stackrel{∧}{y}$=-14x+a,则可预测2017年1月份该地区的平均AQI为36.
| 年份 | 2014 | 2015 | 2016 |
| 1月份平均AQI(y) | 76 | 68 | 48 |
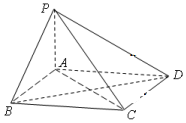 如图,四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD
如图,四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD