Question

19．过抛物线y²=4x的焦点F的直线交抛物线于A，B两点，点O是原点，若|AF|=5，则△AOF的面积为$\frac{5}{2}$．

Answer 1

分析 设A（x₁，y₁）、B（x₂，y₂），算出抛物线的焦点坐标，从而可设直线AB的方程为y=k（x-1），与抛物线方程联解消去x可得y²-$\frac{4}{k}$y-4=0，利用根与系数的关系算出y₁y₂=-4．根据|AF|=5利用抛物线的抛物线的定义算出x₁=4，可得y₁=±4，进而算出|y₁-y₂|=5，最后利用三角形的面积公式加以计算，即可得到△AOB的面积．

解答 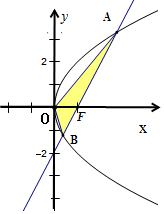解：根据题意，抛物线y²=4x的焦点为F（1，0）．
设直线AB的斜率为k，可得直线AB的方程为y=k（x-1），
由$\left\{\begin{array}{l}{{y}^{2}=4x}\\{y=k（x-1）}\end{array}\right.$消去x，得y²-$\frac{4}{k}$y-4=0，
设A（x₁，y₁）、B（x₂，y₂），由根与系数的关系可得y₁y₂=-4．
根据抛物线的定义，得|AF|=x₁+$\frac{p}{2}$=x₁+1=5，解得x₁=4，
代入抛物线方程得：y₁²=4×4=16，解得y₁=±4，
∵当y₁=4时，由y₁y₂=-4得y₂=-1；当y₁=-4时，由y₁y₂=-4得y₂=1，
∴|y₁-y₂|=5，即AB两点纵坐标差的绝对值等于5．
因此△AOB的面积为：S=_△AOB=S_△AOF+S_△BOF=$\frac{1}{2}$|OF|•|y₁|+$\frac{1}{2}$|OF|•|y₂|
=$\frac{1}{2}$|OF|•|y₁-y₂|=$\frac{1}{2}$×1×5=$\frac{5}{2}$．
故答案为：$\frac{5}{2}$．

点评 本题给出抛物线经过焦点F的弦AB，在已知AF长的情况下求△AOB的面积．着重考查了抛物线定义与标准方程、直线与圆锥曲线位置关系等知识，属于中档题．