Question

18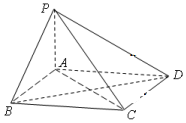．如图，四棱锥P-ABCD中，底面ABCD为菱形，PA⊥平面ABCD
（Ⅰ）证明：平面PBD⊥平面PAC
（Ⅱ）设AP=1，AD=$\sqrt{3}$，∠CBA=60°，求A到平面PBC的距离．

Answer 1

分析 （Ⅰ）推导出BD⊥AC，BD⊥PA，从而BD⊥平面PAC，由此能证明平面PBD⊥平面PAC．
（Ⅱ）由V_A-PBC=V_P-ABC，能求出A到平面PBC的距离．

解答 证明：（Ⅰ）∵四棱锥P-ABCD中，底面ABCD为菱形，
∴BD⊥AC，
∵PA⊥平面ABCD，∴BD⊥PA，
∵AC∩PA=A，∴BD⊥平面PAC，
∵BD?平面PBD，∴平面PBD⊥平面PAC．
解：（Ⅱ）∵AP=1，AD=$\sqrt{3}$，∠CBA=60°，
∴AC=$\sqrt{3}$，${S}_{△ABC}=\frac{\sqrt{3}}{4}•（\sqrt{3}）^{2}=\frac{3\sqrt{3}}{4}$，
∵PC=PB=$\sqrt{P{A}^{2}+A{C}^{2}}=2$，
∴${S}_{△PBC}=\frac{1}{2}×\sqrt{3}×\sqrt{{2}^{2}-（\frac{\sqrt{3}}{2}）^{2}}$=$\frac{\sqrt{39}}{4}$，
设A到平面PBC的距离为h，
∵V_A-PBC=V_P-ABC，
∴$\frac{1}{3}×h×\frac{\sqrt{39}}{4}=\frac{1}{3}×\frac{3\sqrt{3}}{4}×1$，
解得h=$\frac{3\sqrt{13}}{13}$．
∴A到平面PBC的距离为$\frac{3\sqrt{13}}{13}$．

点评 本题考查面面垂直的证明，考查点到平面的距离的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．