题目内容
函数y=2x2-4x+3的值域为 ．
考点：函数的值域
专题：计算题,函数的性质及应用
分析：利用配方法求函数的值域．
解答：
解：y=2x2-4x+3=2（x-1）2+1≥1，
则函数y=2x2-4x+3的值域为[1，+∞）．
故答案为：[1，+∞）．
则函数y=2x2-4x+3的值域为[1，+∞）．
故答案为：[1，+∞）．
点评：本题考查了二次函数求值域的方法，一般用配方法，属于基础题．
练习册系列答案
相关题目
若函数f（x）=ax2+bx+c满足f（4）=f（1），那么（ ）
| A、f（2）＞f（3） |
| B、f（2）=f（3） |
| C、f（2）＜f（3） |
| D、无法比较 |
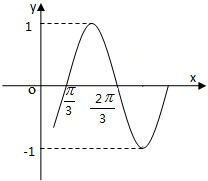若函数y=Asin（ωx+φ）在平面直角坐标系中的图象（部分）如图所示，其中ω＞0，|φ|≤π．