Question

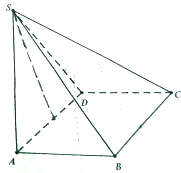如图，四棱锥S-ABCD中，平面SCD⊥底面ABCD，底面ABCD是菱形，AD=2

3

，且SA=SD=

39

．二面角S-AD-B大小为120°
（1）求∠ADC的大小；
（2）求二面角A-SD-C的平面角的正弦值．

Answer 1

考点：二面角的平面角及求法,平面与平面垂直的性质

专题：空间位置关系与距离,空间角

分析：（1）过S作SO⊥平面ABCD，交CD的延长线于点O，取AD中点E，再连接OA，BD，SE，OE，由已知条件∠SEO=60°，SE=

39-3

=6，OE=3，AO=DO=2

3

，由此能求出∠ADC=120°．
（2）由（1）知O、E、B共线，过A作AF⊥OD，则AF⊥平面SOD，作AN⊥SD，并且交SD与点N，连FN，由此∠FNA为二面角A-SD-O的平面角，由此能求出二面角A-SD-C的平面角的正弦值．

解答： 解：（1）∵四棱锥S-ABCD中，平面SCD⊥底面ABCD，底面ABCD是菱形，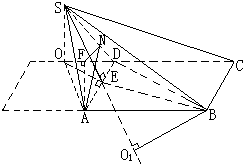
∴过S作SO⊥平面ABCD，交CD的延长线于点O，
取AD中点E，再连接OA，BD，SE，OE，
∵AD=2

3

，且SA=SB=

39

．二面角S-AD-B大小为120°
∴∠SEO=60°，SE=

39-3

=6，OE=3，AO=DO=2

3

，
∴∠ADO=60°，∴∠ADC=120°．
（2）由（1）知O、E、B共线，
过A作AF⊥OD，则AF⊥平面SOD，
作AN⊥SD，并且交SD与点N，连FN，
∴由三垂线定理可得：FN⊥SD，
∴根据二面角的平面角的定义可得：∠FNA为二面角A-SD-O的平面角，
由题意可得：AF=ADsin60°=3，
在△SAD中根据等面积可得：

1

2

×AD×SE=

1

2

×SD×AN，
即

1

2

×2

3

×6=

1

2

×

39

×AN，
所以AN=

12 3

39

=

12 13

13

，
所以sin∠FNA=

AF

AN

=

3

12 3 13

=

13

4

．
故二面角A-SD-C的平面角的正弦值为

13

4

．

点评：本题考查角的大小的求法，考查二面角的平面角的正弦值的求法，解题时要认真审题，注意空间思维能力的培养．