题目内容
数列{an}中,a1=2,an+1=2+
(n∈N*),求证:an<1+
.
| n |
| an |
| n+1 |
考点:数列递推式
专题:点列、递归数列与数学归纳法
分析:把已知的数列递推式变形,把要证的不等式转化为证an+1>
+1,然后利用数学归纳法证明.
| n+1 |
解答:
证明:由an+1=2+
,得an=
,
要证an<1+
,即证
<1+
=
,
∵a1=2,an+1=2+
,∴an+1-2>0,
也就是证an+1>
+1.
下面用数学归纳法证明:
当n=1时,a1=2,a2=2+
=3>
+1,结论成立;
假设当n=k时结论成立,即ak<1+
,
那么,当n=k+1时,ak+1=2+
>2+
=2+
=
+1.
当n=k+1时结论成立.
综上所述,对于任意的n∈N*结论成立.
∴an<1+
.
| n |
| an |
| n |
| an+1-2 |
要证an<1+
| n+1 |
| n |
| an+1-2 |
| n+1 |
| n | ||
|
∵a1=2,an+1=2+
| n |
| an |
也就是证an+1>
| n+1 |
下面用数学归纳法证明:
当n=1时,a1=2,a2=2+
| 1 |
| a1 |
| 1+1 |
假设当n=k时结论成立,即ak<1+
| k+1 |
那么,当n=k+1时,ak+1=2+
| k |
| ak |
| k | ||
1+
|
k(
| ||
| k |
| k+1 |
当n=k+1时结论成立.
综上所述,对于任意的n∈N*结论成立.
∴an<1+
| n+1 |
点评:本题考查了数列递推式,考查了利用数学归纳法证明与自然数有关的命题,解答此题的关键在于把要证的不等式转化为证an+1>
+1,难度较大.
| n+1 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在正方体ABCD-A1B1C1D1中,E、F分别是BB1、CC1的中点,求异面直线AE和BF所成角的余弦值.
如图,在正方体ABCD-A1B1C1D1中,E、F分别是BB1、CC1的中点,求异面直线AE和BF所成角的余弦值.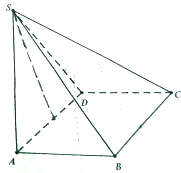 如图,四棱锥S-ABCD中,平面SCD⊥底面ABCD,底面ABCD是菱形,AD=2
如图,四棱锥S-ABCD中,平面SCD⊥底面ABCD,底面ABCD是菱形,AD=2