题目内容
过点（
，-
），且与椭圆
+
=1有相同的焦点的椭圆的标准方程 ．
| 3 |
| 5 |
| y2 |
| 25 |
| x2 |
| 9 |
考点：椭圆的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：求出椭圆
+
=1的焦点，即c=4，可设所求椭圆方程，由a，b，c的关系，和点在椭圆上得到a，b的方程组，解出a，b，进而得到所求椭圆方程．
| y2 |
| 25 |
| x2 |
| 9 |
解答：
解：椭圆
+
=1的焦点为（0，±4），
则所求椭圆的c=4，
可设椭圆方程为
+
=1（a＞b＞0），
则有a2-b2=16，①
再代入点（
，-
），得，
+
=1，②
由①②解得，a2=20，b2=4．
则所求椭圆方程为
+
=1．
故答案为：
+
=1．
| y2 |
| 25 |
| x2 |
| 9 |
则所求椭圆的c=4，
可设椭圆方程为
| y2 |
| a2 |
| x2 |
| b2 |
则有a2-b2=16，①
再代入点（
| 3 |
| 5 |
| 5 |
| a2 |
| 3 |
| b2 |
由①②解得，a2=20，b2=4．
则所求椭圆方程为
| y2 |
| 20 |
| x2 |
| 4 |
故答案为：
| y2 |
| 20 |
| x2 |
| 4 |
点评：本题考查椭圆的方程和性质，考查列方程和解方程的运算能力，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
在△ABC中，a、b、c满足a2+b2+c2=ab+bc+ac，则△ABC一定是（ ）
| A、等边三角形 |
| B、直角三角形 |
| C、锐角三角形 |
| D、钝角三角形 |
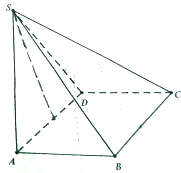如图，四棱锥S-ABCD中，平面SCD⊥底面ABCD，底面ABCD是菱形，AD=2
如图，PA、PB切⊙O于A，B两点，CD切⊙O于点E，交PA，PB于C、D，若⊙O的半径为r，△PCD的周长等于3r，则tan∠APB的值是（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|