题目内容
设函数f(x)=|x+2|-|x-2|
(I)解不等式f(x)≥2;
(Ⅱ)当x∈R,0<y<1时,证明:|x+2|-|x-2|≤
+
.
(I)解不等式f(x)≥2;
(Ⅱ)当x∈R,0<y<1时,证明:|x+2|-|x-2|≤
| 1 |
| y |
| 1 |
| 1-y |
考点:绝对值不等式的解法
专题:计算题,证明题,不等式的解法及应用
分析:(Ⅰ)运用绝对值的定义,去掉绝对值,得到分段函数,再由各段求范围,最后求并集即可;
(II)由分段函数可得f(x)的最大值,再由基本不等式求得
+
的最小值,即可得证.
(II)由分段函数可得f(x)的最大值,再由基本不等式求得
| 1 |
| y |
| 1 |
| 1-y |
解答:
(Ⅰ)解:由已知可得:f(x)=
,
由x≥2时,4>2成立;-2<x<2时,2x≥2,即有x≥1,则为1≤x<2.
所以,f(x)≥2的解集为{x|x≥1};
(II)证明:由(Ⅰ)知,|x+2|-|x-2|≤4,
由于0<y<1,
则
+
=(
+
)[y+(1-y)]=2+
+
≥2+2=4,
则有|x+2|-|x-2|≤
+
.
|
由x≥2时,4>2成立;-2<x<2时,2x≥2,即有x≥1,则为1≤x<2.
所以,f(x)≥2的解集为{x|x≥1};
(II)证明:由(Ⅰ)知,|x+2|-|x-2|≤4,
由于0<y<1,
则
| 1 |
| y |
| 1 |
| 1-y |
| 1 |
| y |
| 1 |
| 1-y |
| 1-y |
| y |
| y |
| 1-y |
则有|x+2|-|x-2|≤
| 1 |
| y |
| 1 |
| 1-y |
点评:本题考查绝对值不等式的解法,考查不等式恒成立,注意转化为函数的最值,考查基本不等式的运用:求最值,考查运算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列命题中,是平面与平面垂直判定定理的是( )
| A、两个平面相交,如果它们所成的二面角是直二面角,那么两个平面相互垂直 |
| B、如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直 |
| C、如果两个平面互相垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面 |
| D、如果一个平面内的一条直线垂直于另一平面的两条相交直线,那么这两个平面互相垂直 |
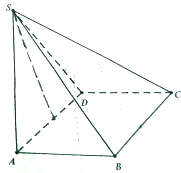 如图,四棱锥S-ABCD中,平面SCD⊥底面ABCD,底面ABCD是菱形,AD=2
如图,四棱锥S-ABCD中,平面SCD⊥底面ABCD,底面ABCD是菱形,AD=2