题目内容
以椭圆
+
=1的左焦点为焦点,以坐标原点为顶点的抛物线方程为( )
| x2 |
| 4 |
| y2 |
| 3 |
| A、y2=-4x |
| B、y2=-2x |
| C、y2=-8x |
| D、y=-x |
考点:椭圆的简单性质,抛物线的标准方程
专题:圆锥曲线的定义、性质与方程
分析:可设抛物线的标准方程为:y2=-2px,其焦点为(-
,0).由椭圆
+
=1,可得左焦点F(-1,0),即为抛物线的焦点,即可得出.
| p |
| 2 |
| x2 |
| 4 |
| y2 |
| 3 |
解答:
解:可设抛物线的标准方程为:y2=-2px,其焦点为(-
,0).
由椭圆
+
=1,可得左焦点F(-1,0),即为抛物线的焦点,
∴-
=-1,解得p=2.
∴抛物线的方程为:y2=-4x.
故选:A.
| p |
| 2 |
由椭圆
| x2 |
| 4 |
| y2 |
| 3 |
∴-
| p |
| 2 |
∴抛物线的方程为:y2=-4x.
故选:A.
点评:本题考查了椭圆与抛物线的标准方程及其性质,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列说法正确的是( )
| A、曲线的切线和曲线的交点有且只有一个 |
| B、过曲线上的一点作曲线的切线,这点一定是切点 |
| C、若f′(x0)不存在,则曲线y=f(x)在点(x0,f(x0))处无切线 |
| D、若y=f(x)在点(x0,f(x0))处有切线,则f′(x0)不一定存在 |
在△ABC中,a、b、c满足a2+b2+c2=ab+bc+ac,则△ABC一定是( )
| A、等边三角形 |
| B、直角三角形 |
| C、锐角三角形 |
| D、钝角三角形 |
下列命题中,是平面与平面垂直判定定理的是( )
| A、两个平面相交,如果它们所成的二面角是直二面角,那么两个平面相互垂直 |
| B、如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直 |
| C、如果两个平面互相垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面 |
| D、如果一个平面内的一条直线垂直于另一平面的两条相交直线,那么这两个平面互相垂直 |
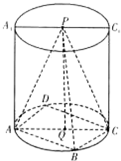 如图,已知圆柱的上、下底面圆心分别为P、Q,AA1与CC1是圆柱的母线,正方形ABCD内接于下底面圆Q,AB=kAA1=2,连接PA、PB、PC.
如图,已知圆柱的上、下底面圆心分别为P、Q,AA1与CC1是圆柱的母线,正方形ABCD内接于下底面圆Q,AB=kAA1=2,连接PA、PB、PC. 如图,在正方体ABCD-A1B1C1D1中,E、F分别是BB1、CC1的中点,求异面直线AE和BF所成角的余弦值.
如图,在正方体ABCD-A1B1C1D1中,E、F分别是BB1、CC1的中点,求异面直线AE和BF所成角的余弦值.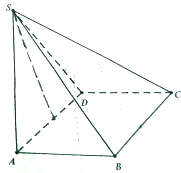 如图,四棱锥S-ABCD中,平面SCD⊥底面ABCD,底面ABCD是菱形,AD=2
如图,四棱锥S-ABCD中,平面SCD⊥底面ABCD,底面ABCD是菱形,AD=2