Question

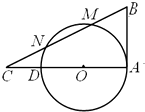AD是⊙O的直径，AB是⊙O切线，A为切点，⊙O上有两点M、N，直线BMN交AD的延长线于点C，BM=MN=NC，AB=2，则⊙O的半径是

 

．

Answer 1

考点：与圆有关的比例线段

专题：直线与圆

分析：由切线长定理知AB²=BM•BM=2BM²，从而得到BC=3

2

，AC=

14

，由切割线定理，知：CD•CA=CN•CM，从而得到CD=

4 14

14

，由此能求出⊙O的半径．

解答： 解：如图，∵AD是⊙O的直径，AB是⊙O切线，A为切点，
⊙O上有两点M、N，直线BMN交AD的延长线于点C，BM=MN=NC，AB=2，
∴AB²=BM•BM=2BM²，
即4=2BM²，解得BM=MN=CN=

2

，∴BC=3

2

，
∴AC=

(3 2 )2-22

=

14

，
由切割线定理，知：CD•CA=CN•CM，
即CD•

14

=

2

•2

2

，解得CD=

4 14

14

，
∴⊙O的半径r=

1

2

(

14

-

4 14

14

)=

5 14

14

．
故答案为：

5

14

14

．

点评：本题考查圆的半径的求法，是中档题，解题时要认真审题，注意切线长定理和切割线定理的合理运用．