题目内容
已知集合U=R,A={x|x2-2ax+a>0},若1∈∁∪A,则a的取值范围是 .
考点:元素与集合关系的判断
专题:集合
分析:先利用条件集合A,求出A的补集,再根据1是补集的元素,代入计算,求出a的值.
解答:
解:∵集合U=R,
∴∁∪A={x|x2-2ax+a≤0}.
又∵1∈∁∪A,
∴1-2a+a≤0,
∴a≥1.
故答案为:a≥1.
∴∁∪A={x|x2-2ax+a≤0}.
又∵1∈∁∪A,
∴1-2a+a≤0,
∴a≥1.
故答案为:a≥1.
点评:本题考查的是集合的补集、元素与集合的关系,要求准确理解概念,细心计算,即可得到本题答案.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在平面直角坐标系中,不等式组
表示的平面区域面积是( )
|
| A、1 | B、2 | C、3 | D、4 |
在公比大于1的等比数列{an}中,a3a7=72,a2+a8=27,则a12=( )
| A、96 | B、64 | C、72 | D、48 |
设a>0,b>0.若
是3a与32b的等比中项,则
+
的最小值为( )
| 3 |
| 2 |
| a |
| 1 |
| b |
| A、8 | ||
| B、4 | ||
| C、1 | ||
D、
|
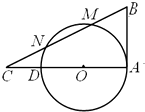 AD是⊙O的直径,AB是⊙O切线,A为切点,⊙O上有两点M、N,直线BMN交AD的延长线于点C,BM=MN=NC,AB=2,则⊙O的半径是
AD是⊙O的直径,AB是⊙O切线,A为切点,⊙O上有两点M、N,直线BMN交AD的延长线于点C,BM=MN=NC,AB=2,则⊙O的半径是