题目内容
以(0,m)间的整数(m>1),m∈N)为分子,以m为分母组成分数集合A1,其所有元素和为a1;以(0,m2)间的整数(m>1),m∈N)为分子,以m2为分母组成不属于集合A1的分数集合A2,其所有元素和为a2;…,依此类推以(0,mn)间的整数(m>1,m∈N)为分子,以mn为分母组成不属于A1,A2,…,An-1的分数集合An,其所有元素和为an;则a1+a2+…+an= .
考点:数列的应用,元素与集合关系的判断,进行简单的合情推理
专题:综合题,等差数列与等比数列
分析:由题意,可根据所给的规则进行归纳,探究出规律,再利用数列的有关知识化简即可得出结论
解答:
解:由题意a1=
+
+…+
a2=
+
+…+
+
+…+
+
+…+
=
+
+…+
-(
+
+…+
)=
+
+…+
-a1,
a3=
+
+…+
-a2-a1,
…
an=
+
+…+
-an-1-…-a2-a1,
由上推理可得a1+a2+…+an=
+
+…+
=
[1+2+3+…+(mn-1)]
由等差数列的求和公式得a1+a2+…+an=
=
故答案为
| 1 |
| m |
| 2 |
| m |
| m-1 |
| m |
a2=
| 1 |
| m2 |
| 2 |
| m2 |
| m-1 |
| m2 |
| m+1 |
| m2 |
| 2m-1 |
| m2 |
| 2m+1 |
| m2 |
| m2-1 |
| m2 |
| 1 |
| m2 |
| 2 |
| m2 |
| m2-1 |
| m2 |
| 1 |
| m |
| 2 |
| m |
| m-1 |
| m |
| 1 |
| m2 |
| 2 |
| m2 |
| m2-1 |
| m2 |
a3=
| 1 |
| m3 |
| 2 |
| m3 |
| m3-1 |
| m3 |
…
an=
| 1 |
| mn |
| 2 |
| mn |
| mn-1 |
| mn |
由上推理可得a1+a2+…+an=
| 1 |
| mn |
| 2 |
| mn |
| mn-1 |
| mn |
| 1 |
| mn |
由等差数列的求和公式得a1+a2+…+an=
| 1 |
| mn |
| [1+(mn-1)]×(mn-1) |
| 2 |
| mn-1 |
| 2 |
故答案为
| mn-1 |
| 2 |
点评:本题考查了等差数列的求和公式,归纳推理,元素与集合关系,考查了探究意识与创新解答问题的能力,本题难度较高,不易入手,惟有耐心细致的列举几个特殊例子才能发现解答本题的规律,此类探究型题可以培养出创新思维的能力

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
以下化简结果不正确的是( )
| A、log35-log315=-1 |
| B、logac•logca=1 |
| C、log42+log48=2 |
| D、(log43+log83)(log32+log92)=-1 |
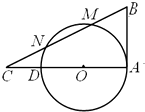 AD是⊙O的直径,AB是⊙O切线,A为切点,⊙O上有两点M、N,直线BMN交AD的延长线于点C,BM=MN=NC,AB=2,则⊙O的半径是
AD是⊙O的直径,AB是⊙O切线,A为切点,⊙O上有两点M、N,直线BMN交AD的延长线于点C,BM=MN=NC,AB=2,则⊙O的半径是