题目内容
已知a、b∈{1,2,…,8,9},且a<b,若ab可以写成两个质数的乘积,则这样的数对{a,b}有 对.
考点:分步乘法计数原理
专题:排列组合
分析:因为1不是质数,所以要进行分类,当a是1时,b是4,6,9,当a是质数是,b一定也是质数,并且要求a<b,问题得以解决.
解答:
解:∵ab可以写成两个质数的乘积,当a是1时,b可以是4,6,9,有3对,a,b都是质数时,且a<b,有
=6对,共有3+6=9对.
故答案为:9.
| ||||
|
故答案为:9.
点评:本题的关键是如何分类,1是特殊元素,于是利用分类计数原理,分类时要不重不漏.

练习册系列答案
相关题目
要得到函数y=2cos5x的图象,只需将函数y=2cos(5x-
)的图象( )
| π |
| 3 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
i为虚数单位,若复数z=
,z的共轭复数为
,则z•
=( )
| 1+2i |
| 2-i |
| z |
| z |
| A、1 | ||
| B、-1 | ||
C、
| ||
D、-
|
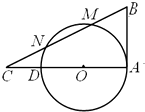 AD是⊙O的直径,AB是⊙O切线,A为切点,⊙O上有两点M、N,直线BMN交AD的延长线于点C,BM=MN=NC,AB=2,则⊙O的半径是
AD是⊙O的直径,AB是⊙O切线,A为切点,⊙O上有两点M、N,直线BMN交AD的延长线于点C,BM=MN=NC,AB=2,则⊙O的半径是