题目内容
若等比数列{an}的前n项和Sn=2n-1+a,则a等于( )
A、-
| ||
B、
| ||
| C、-1 | ||
| D、1 |
考点:等比数列的性质
专题:等差数列与等比数列
分析:由题意可得a1=1+a,当n≥2时,an=2n-2,由题意可得n=1时两式相等,可得a值.
解答:
解:由题意可得a1=S1=20+a=1+a,
当n≥2时,an=Sn-Sn-1=2n-1-2n-2=2n-2,
∵数列{an}为等比数列,
∴1+a=21-2,解得a=-
故选:A
当n≥2时,an=Sn-Sn-1=2n-1-2n-2=2n-2,
∵数列{an}为等比数列,
∴1+a=21-2,解得a=-
| 1 |
| 2 |
故选:A
点评:本题考查等比数列的通项公式与前n项和公式的关系,属基础题.

练习册系列答案
相关题目
在平面直角坐标系中,不等式组
表示的平面区域面积是( )
|
| A、1 | B、2 | C、3 | D、4 |
要得到函数y=2cos5x的图象,只需将函数y=2cos(5x-
)的图象( )
| π |
| 3 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
以下化简结果不正确的是( )
| A、log35-log315=-1 |
| B、logac•logca=1 |
| C、log42+log48=2 |
| D、(log43+log83)(log32+log92)=-1 |
函数f(x)=
的定义域是( )
| ln(x+3) | ||
|
| A、(-3,0) |
| B、(-3,0] |
| C、(-∞,-3)∪(0,+∞) |
| D、(-∞,-3)∪(-3,0) |
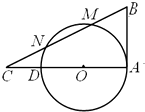 AD是⊙O的直径,AB是⊙O切线,A为切点,⊙O上有两点M、N,直线BMN交AD的延长线于点C,BM=MN=NC,AB=2,则⊙O的半径是
AD是⊙O的直径,AB是⊙O切线,A为切点,⊙O上有两点M、N,直线BMN交AD的延长线于点C,BM=MN=NC,AB=2,则⊙O的半径是