题目内容
已知A(1,0,2),B(1,-3,1),点M在y轴上且到A、B两点的距离相等,则M点坐标为( )
| A、(-1,0,0) |
| B、(0,-1,0) |
| C、(0,0,1) |
| D、(0,1,0) |
考点:空间中的点的坐标
专题:空间位置关系与距离
分析:由于点M在y轴上,可设M(0,y,0).又点M到A、B两点的距离相等,即|MA|=|MB|,利用空间两点间的距离公式即可得出.
解答:
解:∵点M在y轴上,可设M(0,y,0).
又点M到A、B两点的距离相等,即|MA|=|MB|,
∴
=
,
化为y=-1.
∴M(0,-1,0).
故选:B.
又点M到A、B两点的距离相等,即|MA|=|MB|,
∴
| 1+y2+4 |
| 1+(-3-y)2+1 |
化为y=-1.
∴M(0,-1,0).
故选:B.
点评:本题考查了空间中点的坐标特点、空间两点间的距离公式的应用,属于基础题.

练习册系列答案
相关题目
不等式-x2-5x+6≥0的解集为( )
| A、{x|x≤-6或x≥1} |
| B、{x|x≥6或x≤-1} |
| C、{x|-6≤x≤1} |
| D、{x|-1≤x≤6} |
在△ABC中,a、b、c分别是角A、B、C的对边,若a2+b2=2014c2,则
的值为( )
| 2tanA•tanB |
| tanC(tanA+tanB) |
| A、0 | B、1 |
| C、2013 | D、2014 |
不论m为何值,直线(m-1)x+(2m-1)y=m-5恒过定点( )
A、(1,-
| ||
| B、(-2,0) | ||
| C、(2,3) | ||
| D、(9,-4) |
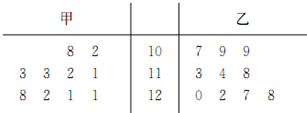 为调查某次考试数学的成绩,随机抽取某中学甲、乙两班各十名同学,获得成绩数据的茎叶图如图(单位:分)
为调查某次考试数学的成绩,随机抽取某中学甲、乙两班各十名同学,获得成绩数据的茎叶图如图(单位:分)