题目内容
求满足下列条件的概率
(1)先后抛掷一枚骰子两次,将得到的点数分别记为a,b.
①求a+b=4的概率;
②求点(a,b)满足a+b≤4的概率;
(2)设a,b均是从区间[0,6]任取的一个数,求满足a+b≤4的概率.
(1)先后抛掷一枚骰子两次,将得到的点数分别记为a,b.
①求a+b=4的概率;
②求点(a,b)满足a+b≤4的概率;
(2)设a,b均是从区间[0,6]任取的一个数,求满足a+b≤4的概率.
考点:几何概型,等可能事件的概率
专题:概率与统计
分析:(1)①先后抛掷一枚骰子两次,求出所有基本事件,满足a+b=4的基本事件,即可求出概率;
②求出满足a+b≤4的基本事件,可求概率;
(2)以面积为测度,分别计算出面积,可求满足a+b≤4的概率.
②求出满足a+b≤4的基本事件,可求概率;
(2)以面积为测度,分别计算出面积,可求满足a+b≤4的概率.
解答:
 解:(1)①先后抛掷一枚骰子两次,基本事件共36个,其中满足a+b=4的基本事件有(1,3),(2,2),(3,1),共3个,
解:(1)①先后抛掷一枚骰子两次,基本事件共36个,其中满足a+b=4的基本事件有(1,3),(2,2),(3,1),共3个,
所以所求概率为
=
;
②满足a+b≤4的基本事件有(1,1),(1,2),(1,3),(2,1),(2,2),(3,1),共6个,所以所求概率为
=
;
(2)如图所示,a,b均是从区间[0,6]任取的一个数,构成一个边长为6的正方形,面积为36;
满足a+b≤4,为图中阴影部分,面积为
×4×4=8,
所以所求概率为
=
.
 解:(1)①先后抛掷一枚骰子两次,基本事件共36个,其中满足a+b=4的基本事件有(1,3),(2,2),(3,1),共3个,
解:(1)①先后抛掷一枚骰子两次,基本事件共36个,其中满足a+b=4的基本事件有(1,3),(2,2),(3,1),共3个,所以所求概率为
| 3 |
| 36 |
| 1 |
| 12 |
②满足a+b≤4的基本事件有(1,1),(1,2),(1,3),(2,1),(2,2),(3,1),共6个,所以所求概率为
| 6 |
| 36 |
| 1 |
| 6 |
(2)如图所示,a,b均是从区间[0,6]任取的一个数,构成一个边长为6的正方形,面积为36;
满足a+b≤4,为图中阴影部分,面积为
| 1 |
| 2 |
所以所求概率为
| 8 |
| 36 |
| 2 |
| 9 |
点评:本题考查概率的计算,确定概率类型是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知偶函数f(x)在区间[0,+∞)单调递减,则满足f(lnx)>f(1)的x取值范围是( )
A、(
| ||
B、(0,
| ||
C、(
| ||
| D、(0,1)∪(e,+∞) |
已知A(1,0,2),B(1,-3,1),点M在y轴上且到A、B两点的距离相等,则M点坐标为( )
| A、(-1,0,0) |
| B、(0,-1,0) |
| C、(0,0,1) |
| D、(0,1,0) |

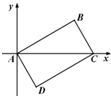 如图,在平面直角坐标系中,已知平行四边形ABCD的三个顶点坐标:A(0,0),B(3,
如图,在平面直角坐标系中,已知平行四边形ABCD的三个顶点坐标:A(0,0),B(3,