题目内容
已知正项等比数列{an}满足:lna1+lna2=4,lna4+lna5=10.
(1)求数列{an}的通项公式;
(2)记Sn=lna1+lna2+…+lnan,数列{bn}满足bn=
,若存在n∈N,使不等式K<(b1+b2+…+bn)(
)n 成立,求实数K的取值范围.
(1)求数列{an}的通项公式;
(2)记Sn=lna1+lna2+…+lnan,数列{bn}满足bn=
| 1 |
| 2Sn |
| 2 |
| 3 |
考点:数列的求和,等比数列的通项公式
专题:等差数列与等比数列
分析:(Ⅰ)由已知得a1a2=e4,a4a5=e10,由此能求出数列{an}的通项公式.
(Ⅱ)由(Ⅰ)知Sn=1+2+3+…+n=
,bn=
=
-
,由此利用裂项求和法能求出实数k的取值范围.
(Ⅱ)由(Ⅰ)知Sn=1+2+3+…+n=
| n(n+1) |
| 2 |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
解答:
解:(Ⅰ)∵正项等比数列{an}满足:lna1+lna2=4,lna4+lna5=10,
∴a1a2=e4,a4a5=e10,
∴q6=e6,由q>0,解得q=e,a1=e,
∴an=en.
(Ⅱ)由(Ⅰ)知Sn=1+2+3+…+n=
,
bn=
=
-
,
∴b1+b2+…+bn=1-
+
-
+…+
-
=1-
=
,
设cn=(b1+b2+…+bn)(
)n,
∴cn=
(
)n,
cn+1-cn=
(
)n+1-
(
)n
=
•(
)n<0,
∴cn>cn+1,
∴数列{cn}单调递减,
(cn)max=c2=
,
∴k<
.
∴a1a2=e4,a4a5=e10,
∴q6=e6,由q>0,解得q=e,a1=e,
∴an=en.
(Ⅱ)由(Ⅰ)知Sn=1+2+3+…+n=
| n(n+1) |
| 2 |
bn=
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
∴b1+b2+…+bn=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
=1-
| 1 |
| n+1 |
=
| n |
| n+1 |
设cn=(b1+b2+…+bn)(
| 2 |
| 3 |
∴cn=
| n |
| n+1 |
| 2 |
| 3 |
cn+1-cn=
| n+1 |
| n+2 |
| 2 |
| 3 |
| n |
| n+1 |
| 2 |
| 3 |
=
| -n2-2n+2 |
| 3(n+1)(n+2) |
| 2 |
| 3 |
∴cn>cn+1,
∴数列{cn}单调递减,
(cn)max=c2=
| 1 |
| 3 |
∴k<
| 1 |
| 3 |
点评:本题考查数列通项公式的求法,考查实数的取值范围的求法,解题时要认真审题,注意裂项求和法的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
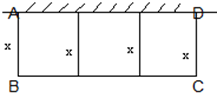 有一批材料可以建成长为200m的围墙,如果用材料在一边靠墙的地方围成一块矩形场地,中间用同样的材料隔成三个面积相等的矩形(如图),求:
有一批材料可以建成长为200m的围墙,如果用材料在一边靠墙的地方围成一块矩形场地,中间用同样的材料隔成三个面积相等的矩形(如图),求: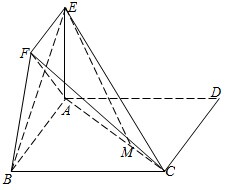 如图,四边形ABCD为正方形,EA⊥平面ABCD,EF∥AB,AB=4,AE=2,EF=1,
如图,四边形ABCD为正方形,EA⊥平面ABCD,EF∥AB,AB=4,AE=2,EF=1,