题目内容
已知函数f(x)=x3+ax2+bx+c在x=-2处取得极值,并且它的图象与直线y=-3x+3在点( 1,0 ) 处相切,
(1)求a,b,c的值;
(2)求f(x)的极值.
(1)求a,b,c的值;
(2)求f(x)的极值.
考点:利用导数研究函数的极值
专题:计算题,导数的概念及应用
分析:(1)求出f′(x),因为函数在x=-2处取得极值,所以f′(-2)=0,又因为函数与直线在点 (1,0 )处相切,所以f′(1)=-3,代入求得两个关于a与b的二元一次方程,求出解集得到a和b,又因为函数过点(1,0),代入求出c的值即可.
(2)由(1)求出的值可得导函数的解析式,分别令其大于、小于0可求增、减区间,即可求出f(x)的极值.
(2)由(1)求出的值可得导函数的解析式,分别令其大于、小于0可求增、减区间,即可求出f(x)的极值.
解答:
解:(1)∵f′(x)=3x2+2ax+b,
∴f′(-2)=3×(-2)2+2a×(-2)+b=0
∴12-4a+b=0 ①
又f′(1)=3+2a+b=-3 ②,
由①②解得a=1,b=-8
又f(x)过点(1,0),
∴13+a×12+b×1+c=0,∴c=6
(2)由(1)知:f(x)=x3+x2-8x+6,所以f′(x)=3x2+2x-8
令3x2+2x-8<0解得-2<x<
,
令3x2+2x-8>0解得x<-2,或x>
故f(x)的单调递增区间为(-∞,-2)和(
,+∞),
f(x)的单调递减区间为(-2,
)
∴在x=-2处取得极大值18,在x=
处取得极小值-
∴f′(-2)=3×(-2)2+2a×(-2)+b=0
∴12-4a+b=0 ①
又f′(1)=3+2a+b=-3 ②,
由①②解得a=1,b=-8
又f(x)过点(1,0),
∴13+a×12+b×1+c=0,∴c=6
(2)由(1)知:f(x)=x3+x2-8x+6,所以f′(x)=3x2+2x-8
令3x2+2x-8<0解得-2<x<
| 4 |
| 3 |
令3x2+2x-8>0解得x<-2,或x>
| 4 |
| 3 |
故f(x)的单调递增区间为(-∞,-2)和(
| 4 |
| 3 |
f(x)的单调递减区间为(-2,
| 4 |
| 3 |
∴在x=-2处取得极大值18,在x=
| 4 |
| 3 |
| 5 |
| 9 |
点评:本题考查学生利用导数研究函数极值的能力,利用导数研究曲线上某点处的切线方程,函数在曲线上某点处的导数值,就是曲线在该点处的切线的斜率,是中档题.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
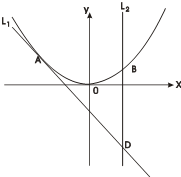 已知A(-1,2)为曲线C:y=2x2上的点,直线l1过点A,且与曲线C相切,
已知A(-1,2)为曲线C:y=2x2上的点,直线l1过点A,且与曲线C相切,