题目内容
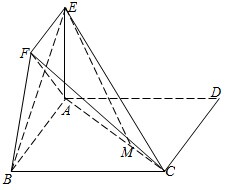如图，四边形ABCD为正方形，EA⊥平面ABCD，EF∥AB，AB=4，AE=2，EF=1，（1）求证：BC⊥AF；
（2）若点M在线段AC上，且满足CM=
| 1 |
| 4 |
考点：直线与平面平行的判定,空间中直线与直线之间的位置关系
专题：空间位置关系与距离
分析：（1）先分别证明出EA⊥BC和BC⊥AB，进而利用线面垂直的判定证明出BC⊥平面ABFE，最后通过线面垂直的性质证明出AF⊥BC．
（2）作MG∥AB，交BC于G，连接FG，通过比例关系证明出EF∥MG，EF=MG，进而通过证明四边形EFGM为平行四边形，证明出FG∥EM，最后利用线面平行的判定定理证明出结论．
（2）作MG∥AB，交BC于G，连接FG，通过比例关系证明出EF∥MG，EF=MG，进而通过证明四边形EFGM为平行四边形，证明出FG∥EM，最后利用线面平行的判定定理证明出结论．
解答：
（1）证明：∵EA⊥平面ABCD，BC?平面ABCD，
∴EA⊥BC，
∵四边形ABCD为正方形，
∴BC⊥AB，
∵AB∩AE=A，AB?平面ABFE，AE?平面ABFE，
∴BC⊥平面ABFE，
∵AF?平面ABFE，
∴AF⊥BC．
（2）证明：作MG∥AB，交BC于G，连接FG，
∵
=
，
∴
=
=1，
∵EF∥AB，EF=1，
∴EF∥MG，EF=MG，
∴四边形EFGM为平行四边形，
∴FG∥EM，
∵EM?平面FBC，FG?平面FBC，
∴EM∥平面FBC．
∴EA⊥BC，
∵四边形ABCD为正方形，
∴BC⊥AB，
∵AB∩AE=A，AB?平面ABFE，AE?平面ABFE，
∴BC⊥平面ABFE，
∵AF?平面ABFE，
∴AF⊥BC．
（2）证明：作MG∥AB，交BC于G，连接FG，
∵
| CM |
| CA |
| 1 |
| 4 |
∴
| MG |
| AB |
| 1 |
| 4 |
∵EF∥AB，EF=1，
∴EF∥MG，EF=MG，
∴四边形EFGM为平行四边形，
∴FG∥EM，
∵EM?平面FBC，FG?平面FBC，
∴EM∥平面FBC．
点评：本题主要考查了线面平行和线面垂直的判定定理的应用．注重了对学生基础知识应用和理解．
练习册系列答案
相关题目
