已知函数f(x)=(ex-1-1)A．当x＜0.有极大值为2-$\frac{4}{e}$B．当x＜0.有极小值为2-$\frac{4}{e}$C．当x＞0.有极大值为0D．当x＞0.有极小值为0 题目和参考答案——青夏教育精英家教网—

题目内容

15．已知函数f（x）=（e^x-1-1）（x-1），则（　　）

	A．	当x＜0，有极大值为2-$\frac{4}{e}$		B．	当x＜0，有极小值为2-$\frac{4}{e}$
	C．	当x＞0，有极大值为0		D．	当x＞0，有极小值为0

分析求出函数的导数，解关于导函数的不等式，求出函数的单调区间，从而求出函数的极值即可．

解答解：f（x）=（e^x-1-1）（x-1），
∴f′（x）=xe^x-1-1，
x＞0时，
令f′（x）＞0，解得：x＞1，令f′（x）＜0，解得：x＜1，
故f（x）在（0，1）递减，在（1，+∞）递增，
故f（x）_极小值=f（1）=0，
故选：D．

点评本题考查了函数的单调性、极值问题，考查导数的应用，是一道基础题．

练习册系列答案

德华书业暑假训练营学年总复习安徽文艺出版社系列答案

金牌作业本南方教与学系列答案

宏翔文化暑假一本通期末加暑假加预习系列答案

6．空间直角坐标系中，设A（-1，2，-3），B（-1，0，2），点M和点A关于y轴对称，则|BM|=3．

3．双曲线y²-$\frac{{x}^{2}}{7}$=1的渐近线方程为（　　）

y=±$\frac{\sqrt{7}}{7}$x

D．

y=±$\frac{1}{7}$x

10．命题“?x∈R，x³-3x＞0”的否定为（　　）

20．在等差数列{a_n}中，a₂=3，a₇=13，数列{b_n}的前n项和为S_n，且S_n=$\frac{4}{3}$（4ⁿ-1）．
（1）求a_n及b_n；
（2）求数列{a_n•b_n}的前n项和T_n．

7．命题“若x＞1，则x²＞1”的逆否命题是若x²≤1，则x≤1．

4．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）过点（$\frac{3}{2}$，-$\frac{\sqrt{6}}{2}$），且离心率为$\frac{\sqrt{3}}{3}$．
（I）求椭圆C的标准方程；
（II）若点A（x₁，y₁），B（x₂，y₂）是椭圆C上的亮点，且x₁≠x₂，点P（1，0），证明：△PAB不可能为等边三角形．

5．

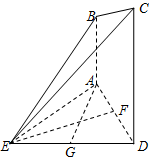如图，在平面ABCD中，AB⊥平面ADE，CD⊥平面ADE，△ADE是等边三角形，AD=DC=2AB=2，F，G分别为AD，DE的中点．
（Ⅰ）求证：EF⊥平面ABCD；
（Ⅱ）求四棱锥E-ABCD的体积；
（Ⅲ）判断直线AG与平面BCE的位置关系，并加以证明．

试题分类