题目内容
20.在等差数列{an}中,a2=3,a7=13,数列{bn}的前n项和为Sn,且Sn=$\frac{4}{3}$(4n-1).(1)求an及bn;
(2)求数列{an•bn}的前n项和Tn.
分析 (1)利用等差数列的通项公式可得an,利用数列递推关系可得bn.
(2)利用“错位相减法”与等比数列的求和公式即可得出.
解答 解:(1)设等差数列{an}的公差为d,∵a2=3,a7=13,
∴a1+d=3,a1+6d=13,
解得a1=1,d=2,
∴an=1+2(n-1)=2n-1.
∵数列{bn}的前n项和为Sn,且Sn=$\frac{4}{3}$(4n-1).
∴b1=S1=4,
n≥2时,bn=Sn-Sn-1=$\frac{4}{3}$(4n-1)-$\frac{4}{3}({4}^{n-1}-1)$=4n,n=1时也成立.
∴bn=4n.
(2)anbn=(2n-1)•4n.
∴数列{an•bn}的前n项和Tn=4+3×42+5×43…+(2n-1)•4n,
4Tn=42+3×43+…+(2n-3)•4n+(2n-1)•4n+1.
∴-3Tn=4+2(42+43+…+4n)-(2n-1)•4n+1=$2×\frac{4({4}^{n}-1)}{4-1}$-4-(2n-1)•4n+1.
∴Tn=$\frac{6n-5}{9}$•4n+1+$\frac{20}{9}$.
点评 本题考查了数列递推关系、等差数列与等比数列的通项公式与求和公式、“错位相减法”方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
15.已知函数f(x)=(ex-1-1)(x-1),则( )
| A. | 当x<0,有极大值为2-$\frac{4}{e}$ | B. | 当x<0,有极小值为2-$\frac{4}{e}$ | ||
| C. | 当x>0,有极大值为0 | D. | 当x>0,有极小值为0 |
5.函数f(x)=$\frac{|x|}{\sqrt{1+{x}^{2}}\sqrt{4+{x}^{2}}}$的最大值为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
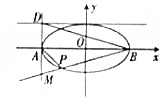 如图,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右顶点分别为A,B,离心率为$\frac{\sqrt{2}}{2}$,直线x=-a与y=b交于点D,且|BD|=3$\sqrt{2}$,过点B作直线l交直线x=-a于点M,交椭圆于另一点P.
如图,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右顶点分别为A,B,离心率为$\frac{\sqrt{2}}{2}$,直线x=-a与y=b交于点D,且|BD|=3$\sqrt{2}$,过点B作直线l交直线x=-a于点M,交椭圆于另一点P.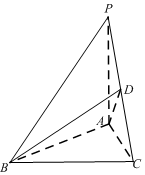 如图,在底面是正三角形的三棱锥P-ABC中,D为PC的中点,PA=AB=1,PB=PC=$\sqrt{2}$.
如图,在底面是正三角形的三棱锥P-ABC中,D为PC的中点,PA=AB=1,PB=PC=$\sqrt{2}$.