��Ŀ����
4����֪��ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�����㣨$\frac{3}{2}$��-$\frac{\sqrt{6}}{2}$������������Ϊ$\frac{\sqrt{3}}{3}$����I������ԲC�ı����̣�
��II������A��x1��y1����B��x2��y2������ԲC�ϵ����㣬��x1��x2����P��1��0����֤������PAB������Ϊ�ȱ������Σ�
���� �����������й���a��b��c�ķ����飬���õ�a��b��ֵ������Բ���̿���
�������PA��PB��֤��|PA|��|PB|������֤������PAB������Ϊ�ȱ������Σ�
��� ��I���⣺�����⣬��$\left\{\begin{array}{l}{\frac{9}{4{a}^{2}}+\frac{6}{4{b}^{2}}=1}\\{\frac{c}{a}=\frac{\sqrt{3}}{3}}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$�����${a}^{2}=\frac{9}{2}��{b}^{2}=3$��
����ԲC�ı�����Ϊ$\frac{2{x}^{2}}{9}+\frac{{y}^{2}}{3}=1$��
��II��֤����֤����A��x1��y1������$2{{x}_{1}}^{2}+3{{y}_{1}}^{2}=9$����x1��[-$\frac{3\sqrt{2}}{2}$��$\frac{3\sqrt{2}}{2}$]��
|PA|=$\sqrt{��{x}_{1}-1��^{2}+{y}_{1}2}$=$\sqrt{��{x}_{1}-1��^{2}+3-\frac{2}{3}{{x}_{1}}^{2}}$=$\sqrt{\frac{1}{3}��{x}_{1}-3��^{2}+1}$��
B��x2��y2����ͬ���ɵ�|PB|=$\sqrt{\frac{1}{3}��{x}_{2}-3��^{2}+1}$����x2��[-$\frac{3\sqrt{2}}{2}$��$\frac{3\sqrt{2}}{2}$]��
y=$\frac{1}{3}��x-3��^{2}+1$��[-$\frac{3\sqrt{2}}{2}$��$\frac{3\sqrt{2}}{2}$]�ϵ�����
����x1=x2?|PA|=|PB|��
��x1��x2����|PA|��|PB|��
���PAB������Ϊ�ȱ������Σ�
���� ���⿼��ֱ������Բ��λ�ù�ϵ�������������빫ʽ�����ã�����ѧ���ļ��������������е��⣮

 һ���㶨ϵ�д�
һ���㶨ϵ�д� ��У��ҵ��ϵ�д�
��У��ҵ��ϵ�д� ���ɶ���ܲ��¿�ֱͨ��Уϵ�д�
���ɶ���ܲ��¿�ֱͨ��Уϵ�д�| A�� | ��x��0���м���ֵΪ2-$\frac{4}{e}$ | B�� | ��x��0���м�СֵΪ2-$\frac{4}{e}$ | ||
| C�� | ��x��0���м���ֵΪ0 | D�� | ��x��0���м�СֵΪ0 |
| A�� | y2=��2$\sqrt{2}$x | B�� | y2=��2x | C�� | y2=��4x | D�� | y2=��4$\sqrt{2}$x |
| A�� | $\frac{10}{17}$ | B�� | $\frac{14}{17}$ | C�� | $\frac{9}{16}$ | D�� | $\frac{7}{9}$ |
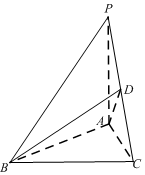 ��ͼ���ڵ������������ε�����P-ABC�У�DΪPC���е㣬PA=AB=1��PB=PC=$\sqrt{2}$��
��ͼ���ڵ������������ε�����P-ABC�У�DΪPC���е㣬PA=AB=1��PB=PC=$\sqrt{2}$��