题目内容
20.在直角坐标系xOy中,曲线C1的参数方程为$\left\{\begin{array}{l}x=2cosα\\ y=2+2sinα\end{array}\right.$(α为参数),M为C1上的动点,P点满足$\overrightarrow{OP}=2\overrightarrow{OM}$,设点P的轨迹为曲线C2.(1)求C1,C2的极坐标方程;
(2)在以O为极点,x轴的正半轴为极轴的极坐标系中,射线$θ=\frac{π}{3}$与C1的异于极点的交点为A,与C2的异于极点的交点为B,求线段AB的长度.
分析 (1)求出C1,C2的普通方程,即可求C1,C2的极坐标方程;
(2)利用极径的意义,求线段AB的长度.
解答 解:(1)设点P(x,y),M(2cosα,2+2sinα),
则由$\overrightarrow{OP}=2\overrightarrow{OM}$得:x=4cosα,y=4+4sinα,消参得:x2+(y-4)2=16.
转化为极坐标方程得:ρ=8sinθ,所以C2的极坐标方程ρ=8sinθ,
同理可得C1的极坐标方程ρ=4sinθ.
(2)在极坐标系,可得$OA=ρ=4sin\frac{π}{3}=2\sqrt{3}$,$OB=ρ=8sin\frac{π}{3}=4\sqrt{3}$,
所以$|AB|=OB-OA=2\sqrt{3}$.
点评 本题考查三种方程的转化,考查极径的意义,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.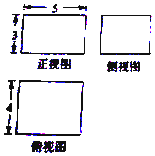 一个四棱柱的三视图如图所示,若该四棱柱的所有顶点都在同一球面上,则这个球的表面积为( )
一个四棱柱的三视图如图所示,若该四棱柱的所有顶点都在同一球面上,则这个球的表面积为( )
 一个四棱柱的三视图如图所示,若该四棱柱的所有顶点都在同一球面上,则这个球的表面积为( )
一个四棱柱的三视图如图所示,若该四棱柱的所有顶点都在同一球面上,则这个球的表面积为( )| A. | 25π | B. | 50π | C. | 100π | D. | 200π |
15.设α,β∈[0,π],且满足sinαcosβ-cosαsinβ=1,则cos(2α-β)的取值范围为( )
| A. | [0,1] | B. | [-1,0] | C. | [-1,1] | D. | $[{-\frac{{\sqrt{2}}}{2},\frac{{\sqrt{2}}}{2}}]$ |
5.下列命题中,错误的是( )
| A. | ?x∈(0,$\frac{π}{2}$),x>sinx | |
| B. | 在△ABC中,若A>B,则sinA>sinB | |
| C. | 函数f(x)=tanx图象的一个对称中心是($\frac{π}{2}$,0) | |
| D. | ?x0∈R,sinx0cosx0=$\frac{\sqrt{2}}{2}$ |
12.已知m=a+blnb,n=b+blna,若a>b>0,则m,n的大小关系是( )
| A. | m>n | B. | m<n | C. | m=n | D. | 大小不确定 |
10.已知等腰梯形ABCD中AB∥CD,AB=2CD=4,∠BAD=60°,双曲线以A,B为焦点,且经过C,D两点,则该双曲线的离心率等于( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | $\sqrt{3}+1$ |
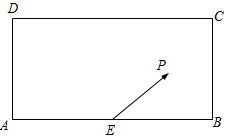 某校兴趣小组在如图所示的矩形区域ABCD内举行机器人拦截挑战赛,在E处按$\overrightarrow{EP}$方向释放机器人甲,同时在A处按某方向释放机器人乙,设机器人乙在Q处成功拦截机器人甲.若点Q在矩形区域ABCD内(包含边界),则挑战成功,否则挑战失败.
某校兴趣小组在如图所示的矩形区域ABCD内举行机器人拦截挑战赛,在E处按$\overrightarrow{EP}$方向释放机器人甲,同时在A处按某方向释放机器人乙,设机器人乙在Q处成功拦截机器人甲.若点Q在矩形区域ABCD内(包含边界),则挑战成功,否则挑战失败.