题目内容
已知关于x的不等式0≤x2-2x+m≤3(m∈R)有且只有一个实数解,函数f(x)=tx,g(x)=2tx2-2(m-t)x+1,若对于任一实数x,f(x)与g(x)至少有一个为正数,则实数t的取值范围是( )
| A、(-∞,0) |
| B、(0,2) |
| C、(2,8) |
| D、(0,8) |
考点:函数的零点与方程根的关系
专题:计算题,压轴题,函数的性质及应用
分析:由关于x的不等式0≤x2-2x+m≤3(m∈R)有且只有一个实数解求出m的值,代入函数化简;当t≤0时,显然不成立;当t>0时,因为g(0)=1>0,所以仅对对称轴进行讨论即可.
解答:
解:∵y=x2-2x+m≥m-1,
又∵关于x的不等式0≤x2-2x+m≤3(m∈R)有且只有一个实数解,
∴m-1=3,
∴m=4,
则g(x)=2tx2-2(4-t)x+1.
当t≤0时,
当x接近+∞时,函数g(x)=2tx2-2(4-t)x+1与f(x)=tx均为负值,
显然不成立,
当t=0时,因g(x)=-8x+1,f(x)=0,故不成立;
当t>0时,
若-
=
≥0,即0<t≤4时,结论显然成立;
若-
=
<0时,只要△=4(4-t)2-8t=4(t-8)(t-2)<0即可,即4<t<8,
故0<t<8.
故选D.
又∵关于x的不等式0≤x2-2x+m≤3(m∈R)有且只有一个实数解,
∴m-1=3,
∴m=4,
则g(x)=2tx2-2(4-t)x+1.
当t≤0时,
当x接近+∞时,函数g(x)=2tx2-2(4-t)x+1与f(x)=tx均为负值,
显然不成立,
当t=0时,因g(x)=-8x+1,f(x)=0,故不成立;
当t>0时,
若-
| b |
| 2a |
| 4-t |
| 2t |
若-
| b |
| 2a |
| 4-t |
| 2t |
故0<t<8.
故选D.
点评:本题主要考查对一元二次函数图象的理解.对于一元二次不等式,一定要注意其开口方向、对称轴和判别式.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
规定a?b=
+2a+b,a、b∈R+,若1?k=4,则函数f(x)=k?x的值域( )
| ab |
| A、(2,+∞) | ||
| B、(1,+∞) | ||
C、[
| ||
D、[
|
已知函数f(x)=sin x+ln x,则f′(1)的值为( )
| A、1-cos 1 |
| B、1+cos 1 |
| C、cos 1-1 |
| D、-1-cos 1 |
如图,在正方形ABCD中,E为AB中点,BF⊥CE于F,那么S△BFC:S正方形ABCD=( )
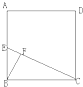

| A、1:3 | B、1:4 |
| C、1:5 | D、1:6 |