题目内容
规定a?b=
+2a+b,a、b∈R+,若1?k=4,则函数f(x)=k?x的值域( )
| ab |
| A、(2,+∞) | ||
| B、(1,+∞) | ||
C、[
| ||
D、[
|
考点:函数的值域
专题:函数的性质及应用
分析:由规定的运算法则知,先求出k的值,再根据法则得到f(x),根据函数的单调性,求出值域.
解答:
解:∵a?b=
+2a+b,a、b∈R+,
∴1?k=
+2+k=4,
解得k=1,
∴k?x=1?x=
+2+x,
∴f(x)=x+
+2,
∴函数f(x)在(0,+∞)为增函数,
∴x+
+2>2,
故函数f(x)的值域为(2,+∞)
故选:A.
| ab |
∴1?k=
| k |
解得k=1,
∴k?x=1?x=
| x |
∴f(x)=x+
| x |
∴函数f(x)在(0,+∞)为增函数,
∴x+
| x |
故函数f(x)的值域为(2,+∞)
故选:A.
点评:本题考查了新定义下的求函数的值域问题,解题时要严格按照规定的定义进行运算,是基本题.

练习册系列答案
相关题目
已知关于x的不等式0≤x2-2x+m≤3(m∈R)有且只有一个实数解,函数f(x)=tx,g(x)=2tx2-2(m-t)x+1,若对于任一实数x,f(x)与g(x)至少有一个为正数,则实数t的取值范围是( )
| A、(-∞,0) |
| B、(0,2) |
| C、(2,8) |
| D、(0,8) |
如图,在正方体ABCD-A1B1C1D1中,异面直线AD1与BA1所成的角为( )
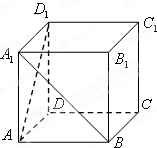

| A、30° | B、45° |
| C、60° | D、90° |
数列{an}为等比数列,且an+2=an+1+2an,an>0,则该数列公比q=( )
| A、1 | ||
| B、2 | ||
C、
| ||
D、
|
下列函数中,既是偶函数又在(0,+∞)上单调递增的是( )
| A、y=ln|x| |
| B、y=-x2 |
| C、y=ex |
| D、y=cosx |