题目内容
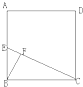
如图,在正方形ABCD中,E为AB中点,BF⊥CE于F,那么S△BFC:S正方形ABCD=( )

| A、1:3 | B、1:4 |
| C、1:5 | D、1:6 |
考点:相似三角形的性质
专题:选作题,立体几何
分析:首先根据题意画出图形,然后根据△BCF∽△ECB及勾股定理求出相似比,得出面积比,又S△EBC=
S正方形ABCD,从而求出S△BFC:S正方形ABCD的值.
| 1 |
| 4 |
解答:
解:设正方形ABCD的边长为2a,
∵E是AB的中点,
∴BE=a,
∴CE=
=
a,
∵BF⊥CE,
∴∠EBC=∠BFC=90°,
∵∠ECB=∠BCF,
∴△BCF∽△EBC.
∴BC:EC=2:
.
∴S△BFC:S△EBC=4:5.
∵S正方形ABCD=4S△EBC,
∴S△BFC:S正方形ABCD=1:5.
故选C.
∵E是AB的中点,
∴BE=a,
∴CE=
| BE2+BC2 |
| 5 |
∵BF⊥CE,
∴∠EBC=∠BFC=90°,
∵∠ECB=∠BCF,
∴△BCF∽△EBC.
∴BC:EC=2:
| 5 |
∴S△BFC:S△EBC=4:5.
∵S正方形ABCD=4S△EBC,
∴S△BFC:S正方形ABCD=1:5.
故选C.
点评:此题考查了相似三角形的判定与性质、正方形的性质以及勾股定理.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
已知关于x的不等式0≤x2-2x+m≤3(m∈R)有且只有一个实数解,函数f(x)=tx,g(x)=2tx2-2(m-t)x+1,若对于任一实数x,f(x)与g(x)至少有一个为正数,则实数t的取值范围是( )
| A、(-∞,0) |
| B、(0,2) |
| C、(2,8) |
| D、(0,8) |
将4个不同颜色的小球全部放入不同标号的3个盒子中,可以有一个或者多个盒子空着的放法种数为( )
| A、96 | B、36 | C、64 | D、81 |
设
为复数z的共轭复数,且
•i=1+2i,则z等于( )
. |
| z |
. |
| z |
| A、2-i | B、2+i |
| C、1+2i | D、1-2i |
设x,y∈R,向量
=(x,1),
=(1,y),
=(2,-4)且
⊥
,
∥
,则x+y=( )
| a |
| b |
| c |
| a |
| c |
| b |
| c |
| A、0 | B、-4 | C、2 | D、4 |
tanθ和tan(
-θ)是方程x2+px+q=0的两根,则p与q的关系是( )
| π |
| 4 |
| A、p+q+1=0 |
| B、p+q-1=0 |
| C、p-q+1=0 |
| D、p-q-1=0 |
阅读下边的程序框图,运行相应的程序,则输出s的值为( )


| A、3 | B、1 | C、0 | D、-1 |