题目内容
已知集合A⊆M={1,2,3,…,11},把满足以下条件:若2k∈A,则2k±1∈A,(k∈Z)的集合A称为好集,则含有至少3个偶数的好集合的个数为( )
| A、34 | B、25 | C、18 | D、32 |
考点:计数原理的应用
专题:排列组合
分析:根据新定义分别讨论含有3个偶数4个偶数和5个偶数时满足集合的个数即可.
解答:
解:根据条件可知,若2∈A,则1,3∈A.若4∈A,则3,5∈A.若6∈A,则5,7∈A.若8∈A,则7,9∈A.若10∈A,则9,11∈A.
考虑将这11个数分组,分成:(1,2,3)、(3,4,5)、(5,6,7)、(7,8,9)、(9,10,11)共五组,且要是进入集合A的话,只能一组一起进.
则含有至少3个偶数可以分为3个偶数,4个人偶数,5个偶数三类,
第一类3个偶数,若为2,4,6时,集合必有1,3,5,7,另外两个奇数9和11,可都有,可有一个,可都没有共4种,
若为4,6,8时,集合必有3,5,7,9另外两个奇数1和11,可都有,可有一个,可都没有共4种,
若为6,8,10时,集合必有5,7,9,11另外两个奇数1和3,可都有,可有一个,可都没有共4种,
若为2,4,8时,集合必有1,3,5,7,9另外1个奇数11,可有,可没有共2种,
若为2,4,10时,集合必有1,3,5,9,11另外1个奇数7,可有,可没有共2种,
若为2,6,8时,集合必有1,3,5,7,9,另外1个奇数1,可有,可没有共2种,
若为2,6,10时,集合必有1,3,5,7,11另外1个奇数9,可有,可没有共2种,
若为2,8,10时,集合必有1,3,7,9,11另外1个奇数5,可有,可没有共2种,
若为4,6,10时,集合必有3,5,7,9,11另外1个奇数1,可有,可没有共2种,
若为4,8,10时,集合必有3,5,7,9,11另外1个奇数1,可有,可没有共2种,
故共有4×3+2×7=26
第二类4个偶数,
若为2,4,6,8,集合必有1,3,5,7,9可能含有11也可能不含11,此时有2种.
若为2,4,6,10,集合则必有1,3,5,7,9,11.此时有1种.
若为2,4,8,10,集合则必有1,3,5,7,9,11,此时有1种.
若为2,6,8,10,集合则必有1,3,5,7,9,11,此时有1种.
若为4,6,8,10,集合则必有3,5,7,9,11.可能含有1也可能不含1,此时有2种.
故共有2+1+1+1+2=7
第三类5个偶数2,4,6,8,10,则必有1,3,5,7,9,11此时有1种.
所以共有26+7+1=34种.
故答案为:A
考虑将这11个数分组,分成:(1,2,3)、(3,4,5)、(5,6,7)、(7,8,9)、(9,10,11)共五组,且要是进入集合A的话,只能一组一起进.
则含有至少3个偶数可以分为3个偶数,4个人偶数,5个偶数三类,
第一类3个偶数,若为2,4,6时,集合必有1,3,5,7,另外两个奇数9和11,可都有,可有一个,可都没有共4种,
若为4,6,8时,集合必有3,5,7,9另外两个奇数1和11,可都有,可有一个,可都没有共4种,
若为6,8,10时,集合必有5,7,9,11另外两个奇数1和3,可都有,可有一个,可都没有共4种,
若为2,4,8时,集合必有1,3,5,7,9另外1个奇数11,可有,可没有共2种,
若为2,4,10时,集合必有1,3,5,9,11另外1个奇数7,可有,可没有共2种,
若为2,6,8时,集合必有1,3,5,7,9,另外1个奇数1,可有,可没有共2种,
若为2,6,10时,集合必有1,3,5,7,11另外1个奇数9,可有,可没有共2种,
若为2,8,10时,集合必有1,3,7,9,11另外1个奇数5,可有,可没有共2种,
若为4,6,10时,集合必有3,5,7,9,11另外1个奇数1,可有,可没有共2种,
若为4,8,10时,集合必有3,5,7,9,11另外1个奇数1,可有,可没有共2种,
故共有4×3+2×7=26
第二类4个偶数,
若为2,4,6,8,集合必有1,3,5,7,9可能含有11也可能不含11,此时有2种.
若为2,4,6,10,集合则必有1,3,5,7,9,11.此时有1种.
若为2,4,8,10,集合则必有1,3,5,7,9,11,此时有1种.
若为2,6,8,10,集合则必有1,3,5,7,9,11,此时有1种.
若为4,6,8,10,集合则必有3,5,7,9,11.可能含有1也可能不含1,此时有2种.
故共有2+1+1+1+2=7
第三类5个偶数2,4,6,8,10,则必有1,3,5,7,9,11此时有1种.
所以共有26+7+1=34种.
故答案为:A
点评:本题主要考查利用集合元素的关系确定集合个数问题,利用分类讨论是解决本题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
已知关于x的不等式0≤x2-2x+m≤3(m∈R)有且只有一个实数解,函数f(x)=tx,g(x)=2tx2-2(m-t)x+1,若对于任一实数x,f(x)与g(x)至少有一个为正数,则实数t的取值范围是( )
| A、(-∞,0) |
| B、(0,2) |
| C、(2,8) |
| D、(0,8) |
数列{an}为等比数列,且an+2=an+1+2an,an>0,则该数列公比q=( )
| A、1 | ||
| B、2 | ||
C、
| ||
D、
|
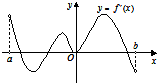 函数f(x)的定义域为开区间(a,b),导函数f′(x)在(a,b)内的图象如图所示,则函数f(x)在开区间(a,b)内有极小值( )
函数f(x)的定义域为开区间(a,b),导函数f′(x)在(a,b)内的图象如图所示,则函数f(x)在开区间(a,b)内有极小值( )| A、2个 | B、1个 | C、3个 | D、4个 |
下列函数中,既是偶函数又在(0,+∞)上单调递增的是( )
| A、y=ln|x| |
| B、y=-x2 |
| C、y=ex |
| D、y=cosx |
将4个不同颜色的小球全部放入不同标号的3个盒子中,可以有一个或者多个盒子空着的放法种数为( )
| A、96 | B、36 | C、64 | D、81 |
tanθ和tan(
-θ)是方程x2+px+q=0的两根,则p与q的关系是( )
| π |
| 4 |
| A、p+q+1=0 |
| B、p+q-1=0 |
| C、p-q+1=0 |
| D、p-q-1=0 |