题目内容
已知函数y=-x2+4x+2,x∈[-1,3],求函数的值域.
考点:二次函数在闭区间上的最值
专题:函数的性质及应用
分析:首先要把函数y=-x2+4x+2的一般式转化成顶点式:y=-(x-2)2+6,函数的对称轴方程为x=2,根据开口方向,自变量距离对称轴越远函数值越小,因此x=2函数值最大,x=-1函数值最小,即求得函数的值域.
解答:
解:函数y=-x2+4x+2=y=-(x-2)2+6,
∴函数的对称轴方程为x=2,
∴根据抛物线的开口方向,自变量距离对称轴越远函数值越小.
因此当x=2时,ymax=6,当x=-1时,ymin=-3,
即求得函数的值域为{y|-3≤y≤6},
故答案为:函数的值域为{y|-3≤y≤6}.
∴函数的对称轴方程为x=2,
∴根据抛物线的开口方向,自变量距离对称轴越远函数值越小.
因此当x=2时,ymax=6,当x=-1时,ymin=-3,
即求得函数的值域为{y|-3≤y≤6},
故答案为:函数的值域为{y|-3≤y≤6}.
点评:本题考查的知识点:二次函数一般式与顶点式的互化,然后根据自变量与对称轴的关系从而确定函数的值域.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
已知O,T,P在△ABC所在平面内,且
+
+
=
,|
|=|
|=|
|,且
•
=
•
=
•
,则点O,T,P依次是△ABC的( )
| OA |
| OB |
| OC |
| 0 |
| TA |
| TB |
| TC |
| PA |
| PB |
| PB |
| PC |
| PC |
| PA |
| A、外心 重心 垂心 |
| B、重心 外心 内心 |
| C、重心 外心 垂心 |
| D、外心 重心 内心 |
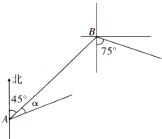 在一次海上联合作战演习中,红方一艘侦察艇发现在北偏东45°方向,相距12n mile的水面上,有蓝方一艘小艇正以每小时10n mile的速度沿南偏东75°方向前进,若侦察艇以每小时14n mile的速度,沿北偏东45°+α方向拦截蓝方的小艇,若要在最短的时间内拦截住,求红方侦察艇所需的时间和角α的正弦值.(注:n mile是海里的英文符号)
在一次海上联合作战演习中,红方一艘侦察艇发现在北偏东45°方向,相距12n mile的水面上,有蓝方一艘小艇正以每小时10n mile的速度沿南偏东75°方向前进,若侦察艇以每小时14n mile的速度,沿北偏东45°+α方向拦截蓝方的小艇,若要在最短的时间内拦截住,求红方侦察艇所需的时间和角α的正弦值.(注:n mile是海里的英文符号)