题目内容
求下列函数的单调区间:
(1)y=x2-5x-6
(2)y=9-x2,x∈[-2,3]
(3)y=-
(4)y=|x+1|
(1)y=x2-5x-6
(2)y=9-x2,x∈[-2,3]
(3)y=-
| 2 |
| x |
(4)y=|x+1|
考点:函数单调性的判断与证明
专题:计算题,函数的性质及应用
分析:(1)(2)是二次函数,单调性取决于对称轴与开口方向;(3)是反比例函数;(4)是绝对值函数,要去绝对值号.
解答:
解:(1)∵y=x2-5x-6=(x-
)2-
,
∴y=x2-5x-6单调增区间为[
,+∞);单调减区间为(-∞,
].
(2)∵y=9-x2,x∈[-2,3],
∴y=9-x2单调增区间为[-2,0];单调减区间为(0,3].
(3)∵y=-
,
∴其单调增区间为(-∞,0),(0,+∞).
(4)∵y=|x+1|,
∴其单调增区间为[-1,+∞);单调减区间为[-∞,-1].
| 5 |
| 2 |
| 49 |
| 4 |
∴y=x2-5x-6单调增区间为[
| 5 |
| 2 |
| 5 |
| 2 |
(2)∵y=9-x2,x∈[-2,3],
∴y=9-x2单调增区间为[-2,0];单调减区间为(0,3].
(3)∵y=-
| 2 |
| x |
∴其单调增区间为(-∞,0),(0,+∞).
(4)∵y=|x+1|,
∴其单调增区间为[-1,+∞);单调减区间为[-∞,-1].
点评:本题考查了基本初等函数的单调性,属于基础题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
设向量
=(2,3),
=(-1,2),若m
+
与
-2
平行,则实数m等于( )
| a |
| b |
| a |
| b |
| a |
| b |
| A、-2 | ||
| B、2 | ||
C、
| ||
D、-
|
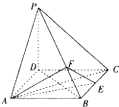 如图,ABCD是正方形,PD⊥平面ABCD,点E是BC中点,点F在PB上,且PE=2FB.
如图,ABCD是正方形,PD⊥平面ABCD,点E是BC中点,点F在PB上,且PE=2FB. 已知函数f(x)=-2
已知函数f(x)=-2 如图所示,在直三棱柱ABC-A1B1C1中,∠ABC=90°,M、N分别为BB1、A1C1的中点.
如图所示,在直三棱柱ABC-A1B1C1中,∠ABC=90°,M、N分别为BB1、A1C1的中点.