题目内容
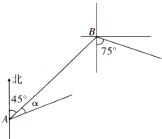在一次海上联合作战演习中，红方一艘侦察艇发现在北偏东45°方向，相距12n mile的水面上，有蓝方一艘小艇正以每小时10n mile的速度沿南偏东75°方向前进，若侦察艇以每小时14n mile的速度，沿北偏东45°+α方向拦截蓝方的小艇，若要在最短的时间内拦截住，求红方侦察艇所需的时间和角α的正弦值．（注：n mile是海里的英文符号）考点：解三角形的实际应用
专题：应用题,解三角形
分析：利用余弦定理，计算AC，BC，根据正弦定理
=
，解得sinα，即可得出结论．
| BC |
| sinα |
| AC |
| sin120° |
解答：
解：如图，设红方侦察艇经过x小时后在C处追上蓝方的小艇，则AC=14x，BC=10x，∠ABC=120°，
根据余弦定理得（14x）2=122+（10x）2-240xcos 120°，
解得x=2．故AC=28，BC=20．
根据正弦定理
=
，
解得sinα=
，即红方侦察艇所需要的时间为2小时，角α的正弦值为
．
解：如图，设红方侦察艇经过x小时后在C处追上蓝方的小艇，则AC=14x，BC=10x，∠ABC=120°，根据余弦定理得（14x）2=122+（10x）2-240xcos 120°，
解得x=2．故AC=28，BC=20．
根据正弦定理
| BC |
| sinα |
| AC |
| sin120° |
解得sinα=
5
| ||
| 14 |
5
| ||
| 14 |
点评：本题考查解三角形的实际应用，考查余弦定理，属于中档题．
练习册系列答案
相关题目