题目内容
5.一个学生通过某次数学测试的概率是$\frac{3}{4}$,他连续测试n次,要保证他至少有一次通过的概率大于0.99,那么n的最小值为4.分析 根据相互独立事件的概率的求法,事件与它的对立事件概率间关系,求得n的最小值.
解答 解:由题意可得 1-${(1-\frac{3}{4})}^{n}$≥0.99,${(\frac{1}{4})}^{n}$≤$\frac{1}{100}$,∴n≥4,
故正整数n的最小值为4,
故答案为:4.
点评 本题主要考查相互独立事件的概率的求法,事件与它的对立事件概率间关系,属于基础题.

练习册系列答案
相关题目
9.曲线f(x)=-$\frac{\sqrt{3}}{3}{x}^{3}$+2在x=1处的切线倾斜角是( )
| A. | $\frac{1}{6}π$ | B. | $\frac{1}{3}π$ | C. | $\frac{5}{6}π$ | D. | $\frac{2}{3}π$ |
17.若函数f(x)=lnx的图象与直线$y=\frac{1}{2}x+a$相切,则a=( )
| A. | 2ln2 | B. | ln2+1 | C. | ln2 | D. | ln2-1 |
14.设甲、乙两楼相距10m,从乙楼底望甲楼顶的仰角为60°,从甲楼顶望乙楼顶的俯角为30°,则甲、乙两楼的高分别是( )
| A. | $\frac{10\sqrt{3}}{3}$m,$\frac{40}{3}$$\sqrt{3}$ m | B. | 10$\sqrt{3}$ m,20$\sqrt{3}$ m | C. | 10($\sqrt{3}$-$\sqrt{2}$) m,20$\sqrt{3}$ m | D. | 10$\sqrt{3}$ m,$\frac{40}{3}$$\sqrt{3}$ m |
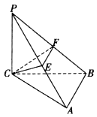 如图,已知在三棱锥P-ABC中,PC⊥平面ABC,AB⊥BC,若PC=BC=8,AB=4,E,F分别是PA,PB的中点,设三棱锥P-CEF的外接球的球心为O,则△AOB的面积为8$\sqrt{5}$.
如图,已知在三棱锥P-ABC中,PC⊥平面ABC,AB⊥BC,若PC=BC=8,AB=4,E,F分别是PA,PB的中点,设三棱锥P-CEF的外接球的球心为O,则△AOB的面积为8$\sqrt{5}$. 如图,渔船甲位于岛屿A的南偏西60°方向的B处,且与岛屿A相距6海里,渔船乙以5 海里/小时的速度从岛屿A出发沿正北方向航行,若渔船甲同时从B处出发沿北偏东α的方向追赶渔船乙,刚好用2小时追上.
如图,渔船甲位于岛屿A的南偏西60°方向的B处,且与岛屿A相距6海里,渔船乙以5 海里/小时的速度从岛屿A出发沿正北方向航行,若渔船甲同时从B处出发沿北偏东α的方向追赶渔船乙,刚好用2小时追上.