题目内容
9．曲线f（x）=-$\frac{\sqrt{3}}{3}{x}^{3}$+2在x=1处的切线倾斜角是（ ）| A． | $\frac{1}{6}π$ | B． | $\frac{1}{3}π$ | C． | $\frac{5}{6}π$ | D． | $\frac{2}{3}π$ |
分析 根据题意求出函数的导数，进而求出切线的斜率，即可得到切线的倾斜角．
解答 解：由题意可得：曲线的方程为：y=-$\frac{\sqrt{3}}{3}$x3+2x，
所以y′=-$\sqrt{3}$x2，
所以K切=y′|x=1=-$\sqrt{3}$，
所以曲线y=-$\frac{\sqrt{3}}{3}$x3+2x在x=1处的切线的倾斜角是$\frac{2}{3}$π．
故选：D．
点评 本题主要考查导数的几何意义，以及求导公式．
练习册系列答案
相关题目
20．用数列归纳法证明$\frac{1}{2}+cosα+cos2α+…+cosnα=\frac{{sin（n+\frac{1}{2}）α}}{{2sin\frac{α}{2}}}$时，验证n=1时，左边式子为（ ）
| A． | $\frac{1}{2}$ | B． | cosα | C． | $\frac{1}{2}+cosα$ | D． | $\frac{{sin\frac{3}{2}α}}{{2sin\frac{α}{2}}}$ |
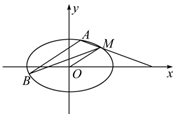如图，已知椭圆C的中心在原点，它的一个焦点与抛物线${y^2}=4\sqrt{6}x$的焦点相同，又椭圆C上有一点M（2，1），直线l平行于OM且与椭圆C交于A，B两点，连接MA，MB．
如图所示的三棱柱ABC-A1B1C1中，底面是正三角形，侧棱BB1⊥面ABC，D是棱BC的中点，点M在棱BB1上，且CM⊥AC1．