题目内容
16．
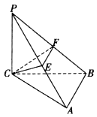如图，已知在三棱锥P-ABC中，PC⊥平面ABC，AB⊥BC，若PC=BC=8，AB=4，E，F分别是PA，PB的中点，设三棱锥P-CEF的外接球的球心为O，则△AOB的面积为8$\sqrt{5}$．
分析 过O作OH⊥平面PCF，则垂足H为PC中点，证明AB⊥平面PBC得出OH∥AB，故而O到AB的距离为BH的长，代入面积公式即可求出答案．
解答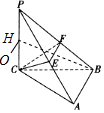 
解：∵PC=CB，F是PB的中点，
∴CF⊥PF，即△PCF是直角三角形．
过O作OH⊥平面PCF，垂足为H，则H是PC的中点，
∵PC⊥平面ABC，AB?平面ABC，
∴PC⊥AB，又AB⊥BC，PC∩BC=C，
∴AB⊥平面PBC，又OH⊥平面PBC，
∴OH∥AB，
连结BH，则BH为O到AB的距离，
由勾股定理得BH=$\sqrt{B{C}^{2}+C{H}^{2}}$=4$\sqrt{5}$，
∴S△OAB=$\frac{1}{2}×AB×BH$=$\frac{1}{2}×4×4\sqrt{5}$=8$\sqrt{5}$．
故答案为：8$\sqrt{5}$．
点评 本题考查了空间距离的计算，棱锥与球的位置关系，属于中档题．
练习册系列答案
怎样学好牛津英语系列答案
相关题目
20．用数列归纳法证明$\frac{1}{2}+cosα+cos2α+…+cosnα=\frac{{sin（n+\frac{1}{2}）α}}{{2sin\frac{α}{2}}}$时，验证n=1时，左边式子为（ ）
| A． | $\frac{1}{2}$ | B． | cosα | C． | $\frac{1}{2}+cosα$ | D． | $\frac{{sin\frac{3}{2}α}}{{2sin\frac{α}{2}}}$ |
如图所示的三棱柱ABC-A1B1C1中，底面是正三角形，侧棱BB1⊥面ABC，D是棱BC的中点，点M在棱BB1上，且CM⊥AC1．
11．已知在平面直角坐标系中，曲线f（x）=alnx+x在x=a处的切线过原点，则a=（ ）
| A． | 1 | B． | e | C． | $\frac{1}{e}$ | D． | 0 |
8．某工厂为了对新研发的一种产品进行合理定价，将该定价按事先拟定的价格进行试销，得到如下数据：
（1）求回归直线方程$\hat y=bx+a$；
（2）预计在今后的销售中，销量与单价仍然服从（1）中的关系，且该产品的成本是4元/件，为使工厂获得最大利润，该产品的单价应定为多少元？
附：$b=\frac{{\sum_{i=1}^n{（{{x_i}-\overline x}）}（{{y_i}-\overline y}）}}{{\sum_{i=1}^n{{{（{{x_i}-\overline x}）}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}，a=\overline y-b\overline x$．
| 单价x（元） | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
| 销量y（元） | 90 | 84 | 83 | 80 | 75 | 68 |
（2）预计在今后的销售中，销量与单价仍然服从（1）中的关系，且该产品的成本是4元/件，为使工厂获得最大利润，该产品的单价应定为多少元？
附：$b=\frac{{\sum_{i=1}^n{（{{x_i}-\overline x}）}（{{y_i}-\overline y}）}}{{\sum_{i=1}^n{{{（{{x_i}-\overline x}）}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}，a=\overline y-b\overline x$．