题目内容
函数y=4cosx-e|x|(e为自然对数的底数)的图象可能是( )
A、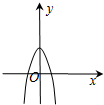 |
B、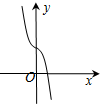 |
C、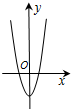 |
D、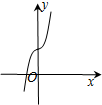 |
考点:函数的图象
专题:函数的性质及应用
分析:先验证函数y=4cosx-e|x|是否具备奇偶性,排除一些选项,在取特殊值x=0时代入函数验证即可得到答案.
解答:
解:∵函数y=4cosx-e|x|,
∴f(-x)=4cos(-x)-e|-x|=4cosx-e|x|=f(x),
函数y=4cosx-e|x|为偶函数,图象关于y轴对称,排除BD,
又f(0)=y=4cos0-e|0|=4-1=3,
只有A适合,
故选:A.
∴f(-x)=4cos(-x)-e|-x|=4cosx-e|x|=f(x),
函数y=4cosx-e|x|为偶函数,图象关于y轴对称,排除BD,
又f(0)=y=4cos0-e|0|=4-1=3,
只有A适合,
故选:A.
点评:本题主要考查函数的图象,关于函数图象的选择题,通常先验证奇偶性,排除一些选项,再代特殊值验证,属于中档题.

练习册系列答案
相关题目
已知关于x方程x3+ax2+bx+c=0的三个根可以作为一椭圆,一双曲线,一抛物线的离心率,则
的取值范围( )
| b |
| a |
A、(-2,-
| ||
| B、(-2,-1) | ||
C、(-1,-
| ||
D、(-∞,-
|
