题目内容
有甲、乙两城，甲城位于一直线河岸，乙城离岸40km，乙城到河岸的垂足B与甲城相距50km，两城要在此河边合舍一个水厂取水，从水厂到甲城和乙城的水管费用分别为每千米500元和我700元，则水厂甲城的距离为 千米，才能使水管费用最省？
考点：函数模型的选择与应用
专题：应用题,导数的综合应用
分析：先确定AC与DC的长，在根据水管费用即可建立总的水管费用函数解析式；利用导数求出函数最值，即可确定供水站C建在岸边何处才能使水管费用最省．
解答：
解：设甲在A处，乙在D处，供水站C，总的水管费用为y元，CB=x，BD=40，AC=50-x，
∴DC=
依题意有：y=500（50-x）+700
（0＜x＜50）
得y′=-500+
，
令y′=0，解得x=
y在（0，
）单调递减，在（
，50）单调递增上，
函数在x=
（km）处取得最小值，此时AC=50-
（km）
故答案为：50-
．
∴DC=
| x2+402 |
依题意有：y=500（50-x）+700
| x2+402 |
得y′=-500+
| 700x | ||
|
令y′=0，解得x=
50
| ||
| 3 |
y在（0，
50
| ||
| 3 |
50
| ||
| 3 |
函数在x=
50
| ||
| 3 |
50
| ||
| 3 |
故答案为：50-
50
| ||
| 3 |
点评：本题考查导数在生活中优化问题的应用，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
函数y=4cosx-e|x|（e为自然对数的底数）的图象可能是（ ）
A、 |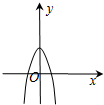
B、 |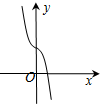
C、 |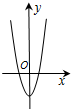
D、 |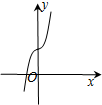
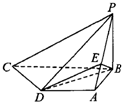如图所示，四棱锥P-ABCD中，PB⊥平面ABCD，底面ABCD为直角梯形，AD∥BC，AB⊥BC，AB=AD=PB=3，点E在棱PA上，且PE=2EA，则平面ABE与平面BED的夹角的余弦值为