题目内容
已知圆x2+y2-6x-7=0与抛物线C:y2=2px(p>0)的准线相切
(Ⅰ)求抛物线C的方程
(Ⅱ)过抛物线C的焦点F的直线交抛物线于A,B两点,若|AB|=7,求线段AB的中点M到y轴的距离.
(Ⅰ)求抛物线C的方程
(Ⅱ)过抛物线C的焦点F的直线交抛物线于A,B两点,若|AB|=7,求线段AB的中点M到y轴的距离.
考点:圆与圆锥曲线的综合,抛物线的标准方程,直线与圆锥曲线的关系
专题:圆锥曲线的定义、性质与方程
分析:(Ⅰ)求出圆的圆心与半径,利用y2=2px(p>0)的准线相切,求出p,得到抛物线方程.
(Ⅱ)求出抛物线C的焦点坐标为(1,0),准线方程为x=-1,求出抛物线定义知线段AB的中点M到准线的距离,然后求解线段AB的中点M到y轴的距离.
(Ⅱ)求出抛物线C的焦点坐标为(1,0),准线方程为x=-1,求出抛物线定义知线段AB的中点M到准线的距离,然后求解线段AB的中点M到y轴的距离.
解答:
解:(Ⅰ)圆x2+y2-6x-7=0,即(x-3)2+y2=16,所以圆心(3,0),半径为4,
抛物线的准线方程为x=-
,依题意,有3-(-
)=4,得p=2,
故抛物线方程为y2=4x;------(6分)
(Ⅱ)由(Ⅰ)知,抛物线C的焦点坐标为(1,0),准线方程为x=-1,
由抛物线定义知线段AB的中点M到准线的距离为
(|,
故线段AB的中点M到y轴的距离d=
-1=
.------(12分)
抛物线的准线方程为x=-
| p |
| 2 |
| p |
| 2 |
故抛物线方程为y2=4x;------(6分)
(Ⅱ)由(Ⅰ)知,抛物线C的焦点坐标为(1,0),准线方程为x=-1,
由抛物线定义知线段AB的中点M到准线的距离为
| 1 |
| 2 |
故线段AB的中点M到y轴的距离d=
| 7 |
| 2 |
| 5 |
| 2 |
点评:本题考查圆的方程与抛物线方程的综合应用,点到直线的距离,考查分析问题解决问题的能力.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案
相关题目
若θ是第三象限,且cos
>0,则
是( )
| θ |
| 2 |
| θ |
| 2 |
| A、第一象限角 |
| B、第二象限角 |
| C、第三象限角 |
| D、第四象限角 |
函数y=4cosx-e|x|(e为自然对数的底数)的图象可能是( )
A、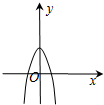 |
B、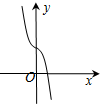 |
C、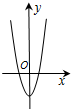 |
D、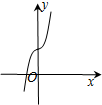 |
对任意x,y∈R,函数f(x)都满足f(x+y)=f(x)+f(y)+2恒成立,则f(5)+f(-5)等于( )
| A、0 | B、-4 | C、-2 | D、2 |
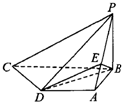 如图所示,四棱锥P-ABCD中,PB⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,AB⊥BC,AB=AD=PB=3,点E在棱PA上,且PE=2EA,则平面ABE与平面BED的夹角的余弦值为
如图所示,四棱锥P-ABCD中,PB⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,AB⊥BC,AB=AD=PB=3,点E在棱PA上,且PE=2EA,则平面ABE与平面BED的夹角的余弦值为