题目内容
提高穿山隧道的车辆通行能力可有效改善交通状况,在一般情况下,隧道内的车流速度v(单位:千米、小时)是车流密度x(单位:辆/千米,车流密度指每千米道路上车辆的数量)的函数.当隧道内的车流密度达到210辆/千米时,将造成堵塞,此时车流速度为0;当车流密度不超过30辆/千米时,车流速度为60千米/小时,研究表明:当30≤x≤210时,车流速度v是车流密度x的一次函数.
(Ⅰ)当0≤x≤210时,求函数v(x)的表达式;
(Ⅱ)当车流密度x为多大时,车流量(单位时间内通过某观测点的车辆数,单位:辆/小时)f(x)=x•v(x)可以达到最大,并求出最大值.
(Ⅰ)当0≤x≤210时,求函数v(x)的表达式;
(Ⅱ)当车流密度x为多大时,车流量(单位时间内通过某观测点的车辆数,单位:辆/小时)f(x)=x•v(x)可以达到最大,并求出最大值.
考点:函数模型的选择与应用
专题:应用题,函数的性质及应用
分析:(I)根据题意,函数v(x)表达式为分段函数的形式,关键在于求函数v(x)在60≤x≤600时的表达式,根据一次函数表达式的形式,用待定系数法可求得;
(II)由(Ⅰ)可知f(x)=
,分段求最值,即可得出结论.
(II)由(Ⅰ)可知f(x)=
|
解答:
解:(Ⅰ)由题意知,当0≤x≤30时,v(x)=60;
当30≤x≤210时,设v(x)=ax+b,
由已知可得
,解得
.
所以函数v(x)=
.…(6分)
(Ⅱ)由(Ⅰ)可知f(x)=
当0≤x≤30时,f(x)=60x为增函数,
∴当x=30时,其最大值为1800.…(9分)
当30≤x≤210时,f(x)=-
x2+70x=-
(x-105)2+3675,
当x=105时,其最大值为3675.…(11分)
综上,当车流密度为105辆/千米时,车流量最大,最大值为3675辆.…(12分)
当30≤x≤210时,设v(x)=ax+b,
由已知可得
|
|
所以函数v(x)=
|
(Ⅱ)由(Ⅰ)可知f(x)=
|
当0≤x≤30时,f(x)=60x为增函数,
∴当x=30时,其最大值为1800.…(9分)
当30≤x≤210时,f(x)=-
| 1 |
| 3 |
| 1 |
| 3 |
当x=105时,其最大值为3675.…(11分)
综上,当车流密度为105辆/千米时,车流量最大,最大值为3675辆.…(12分)
点评:本题给出车流密度的实际问题,求车流量的最大值及相应的车流密度,着重考查了函数、最值等基础知识,同时考查运用数学知识解决实际问题的能力,属于中档题.

练习册系列答案
相关题目
函数y=4cosx-e|x|(e为自然对数的底数)的图象可能是( )
A、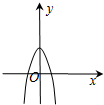 |
B、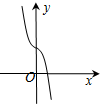 |
C、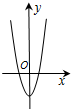 |
D、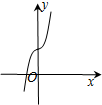 |
对任意x,y∈R,函数f(x)都满足f(x+y)=f(x)+f(y)+2恒成立,则f(5)+f(-5)等于( )
| A、0 | B、-4 | C、-2 | D、2 |