题目内容
已知关于x方程x3+ax2+bx+c=0的三个根可以作为一椭圆,一双曲线,一抛物线的离心率,则
的取值范围( )
| b |
| a |
A、(-2,-
| ||
| B、(-2,-1) | ||
C、(-1,-
| ||
D、(-∞,-
|
考点:抛物线的简单性质,双曲线的简单性质
专题:不等式的解法及应用,圆锥曲线的定义、性质与方程
分析:由抛物线的离心率为1,求得a,b和c的关系代入函数解析式消去c,整理成f(x)=(x-1)(x2+x+1)+a(x+1)(x-1)+b(x-1)的形式,设g(x)=x2+(a+1)x+1+a+b椭圆和双曲线的离心率的范围确定两根的范围确定g(0)>0,g(1)<0,最后利用线性规划求得
的范围.
| b |
| a |
解答:
 解:由抛物线的离心率为1,可得1+a+b+c=0,
解:由抛物线的离心率为1,可得1+a+b+c=0,
即有c=-1-a-b,代入f(x)=x3+ax2+bx+c,
即f(x)=x3+ax2+bx-1-a-b
=(x-1)(x2+x+1)+a(x+1)(x-1)+b(x-1)
=(x-1)[x2+(a+1)x+1+a+b],
设g(x)=x2+(a+1)x+1+a+b,
则g(x)=0的两根满足0<x1<1,x2>1,
即有g(0)=1+a+b>0且g(1)=3+2a+b<0,
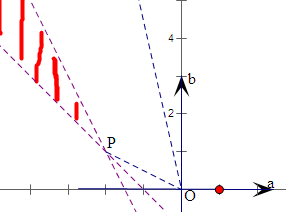
如图,作出点(a,b)满足的可行域,
即为图中斜线部分(不含边界),
=
表示(a,b)与原点的斜率,
求得P(-2,1),
由于OP的斜率为-
,
由图象可得-2<
<-
.
故选A.
 解:由抛物线的离心率为1,可得1+a+b+c=0,
解:由抛物线的离心率为1,可得1+a+b+c=0,即有c=-1-a-b,代入f(x)=x3+ax2+bx+c,
即f(x)=x3+ax2+bx-1-a-b
=(x-1)(x2+x+1)+a(x+1)(x-1)+b(x-1)
=(x-1)[x2+(a+1)x+1+a+b],
设g(x)=x2+(a+1)x+1+a+b,
则g(x)=0的两根满足0<x1<1,x2>1,
即有g(0)=1+a+b>0且g(1)=3+2a+b<0,
如图,作出点(a,b)满足的可行域,
即为图中斜线部分(不含边界),
| b |
| a |
| b-0 |
| a-0 |
求得P(-2,1),
由于OP的斜率为-
| 1 |
| 2 |
由图象可得-2<
| b |
| a |
| 1 |
| 2 |
故选A.
点评:本题主要考查了函数的零点和根的分布,圆锥曲线的共同特征,线性规划的基础知识.考查基础知识的综合运用.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
函数y=4cosx-e|x|(e为自然对数的底数)的图象可能是( )
A、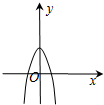 |
B、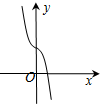 |
C、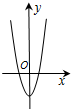 |
D、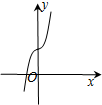 |
对任意x,y∈R,函数f(x)都满足f(x+y)=f(x)+f(y)+2恒成立,则f(5)+f(-5)等于( )
| A、0 | B、-4 | C、-2 | D、2 |
设
,
是单位向量,则“
•
>0”是“
和
的夹角为锐角”的( )
| a |
| b |
| a |
| b |
| a |
| b |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
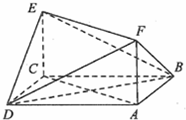 如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=