题目内容
函数y=
的定义域为 .
| 3 |
| 1+2sinx |
考点:函数的定义域及其求法
专题:函数的性质及应用
分析:根据函数成立的条件即可求函数的定义域.
解答:
解:要使函数有意义,则1+2sinx≠0,即sinx≠-
,
即x≠2kπ+
且x≠2kπ+
,k∈Z,
故函数的定义域为{x|x≠2kπ+
且x≠2kπ+
,k∈Z},
故答案为:{x|x≠2kπ+
且x≠2kπ+
,k∈Z}
| 1 |
| 2 |
即x≠2kπ+
| 7π |
| 6 |
| 11π |
| 6 |
故函数的定义域为{x|x≠2kπ+
| 7π |
| 6 |
| 11π |
| 6 |
故答案为:{x|x≠2kπ+
| 7π |
| 6 |
| 11π |
| 6 |
点评:本题主要考查函数的定义域的求解,要求熟练掌握常见函数成立的条件

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数y=4cosx-e|x|(e为自然对数的底数)的图象可能是( )
A、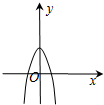 |
B、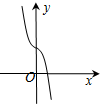 |
C、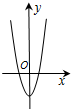 |
D、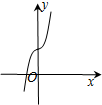 |
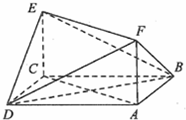 如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=