题目内容
函数f(x)=2sinπx与函数g(x)=
的图象所有交点的橫坐标之和为 .
| 3 | x-1 |
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:根据函数f(x)和g(x)的图象特点,利用数形结合得到结论.
解答:
解:函数g(x)=
关于(1,0)对称,函数g(x)单调递增,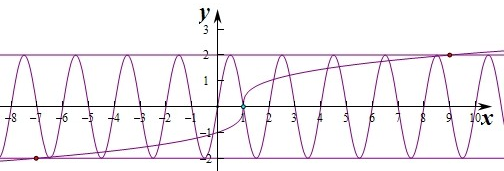
且函数f(x)=2sinπx也关于(1,0)对称,
由
=2,解得x-1=8,即x=9,
由
=-2,解得x-1=-8,即x=-7,
∴两个函数f(x)和g(x)共有17个交点,除(1,0)外,其他16个交点关于(1,0)对称,
设对称的两个点的横坐标分别为a,b,
则
=1,即a+b=2,
∴函数f(x)=2sinπx与函数g(x)=
的图象所有交点的橫坐标之和为:
8(a+b)+1=8×2+1=17.
故答案为:17.
| 3 | x-1 |

且函数f(x)=2sinπx也关于(1,0)对称,
由
| 3 | x-1 |
由
| 3 | x-1 |
∴两个函数f(x)和g(x)共有17个交点,除(1,0)外,其他16个交点关于(1,0)对称,
设对称的两个点的横坐标分别为a,b,
则
| a+b |
| 2 |
∴函数f(x)=2sinπx与函数g(x)=
| 3 | x-1 |
8(a+b)+1=8×2+1=17.
故答案为:17.
点评:本题主要考查函数图象的交点问题,根据函数f(x)和g(x)的图象的对称性,利用数形结合是解决本题的关键,考查学生的作图分析能力.综合性较强,难度较大.

练习册系列答案
相关题目
函数g(x)=lnx-
的零点所在区间是( )
| 1 |
| x |
| A、(0,1) |
| B、(1,2) |
| C、(2,3) |
| D、(3,4) |
若集合A={x∈R|y=lg(2-x)},B={y∈R|y=2x-1,x∈A},则∁R(A∩B)=( )
| A、R |
| B、(-∞,0]∪[2,+∞) |
| C、[2,+∞) |
| D、(-∞,0] |
已知三角形ABC中,
•
<0,则三角形ABC的形状为( )
| BA |
| BC |
| A、钝角三角形 |
| B、直角三角形 |
| C、锐角三角形 |
| D、等腰直角三角形 |
 如图,已知椭圆
如图,已知椭圆