Question

已知函数f(x)=

x2+2x，x≥0 -x2+2x，x＜0

，则使f（a²）＞f（4a）成立的实数a的取值范围是

 

．

Answer 1

考点：函数单调性的性质

专题：函数的性质及应用

分析：对f（x）变形后画出其草图，根据图象可判断f（x）在R上的单调性，利用单调性可去掉不等式中的符号“f”，解二次不等式即可得到答案．

解答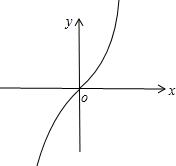： 解：x≥0时，f（x）=x²+2x=（x+1）²-1，
x＜0时，f（x）=-x²+2x=-（x-1）²+1，
作出f（x）的草图如图所示：
由图象可知f（x）在R上单调递增，
∴f由（a²）＞f（4a）可得a²＞4a，解得a＞4或a＜0，
∴实数a的取值范围是（-∞，0）∪（4，+∞），
故答案为：（-∞，0）∪（4，+∞）．

点评：本题考查函数单调性的应用、抽象不等式的求解，利用函数单调性化抽象不等式为具体不等式是解决问题的关键所在．