题目内容
已知
=(2cos
,1),
=(sin
,0),f(x)=
•
.
(Ⅰ)求函数f(x)的单调递增区间;
(Ⅱ)若将f(x)的图象平移
个单位(可向上、下、左、右平移,且仅可选择一种方向平移一次)得到g(x),求h(x)=f(x)g(x)的最小值.
| a |
| x |
| 2 |
| b |
| x |
| 2 |
| a |
| b |
(Ⅰ)求函数f(x)的单调递增区间;
(Ⅱ)若将f(x)的图象平移
| 2π |
| 3 |
考点:函数y=Asin(ωx+φ)的图象变换,平面向量数量积的运算,三角函数中的恒等变换应用
专题:三角函数的图像与性质
分析:(Ⅰ)由题意利用两个向量的数量积公式可得 f(x)=
•
=sinx,从而求得函数的增区间.
(Ⅱ)按方案①,把f(x)的图象向上平移
个单位,求出g(x)以及h(x)取得最小值.按方案②,把f(x)的图象向下平移
个单位,求出g(x)以及h(x)取得最小值.按方案③,把f(x)的图象向左平移
个单位,求出g(x)以及h(x)取得最小值.按方案④,把f(x)的图象向右平移
个单位,求出g(x)以及h(x)取得最小值.
| a |
| b |
(Ⅱ)按方案①,把f(x)的图象向上平移
| 2π |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
解答:
解:(Ⅰ)由题意可得 f(x)=
•
=2cos
•sin
=sinx,故函数的增区间为[2kπ-
,2kπ+
],k∈z.
(Ⅱ)方案①若把f(x)的图象向上平移
个单位,得到g(x)=sinx+
,
∴h(x)=sinx(sinx+
)=(sinx+
)2-
,
∴当sinx=-1,即 x=2kπ-
,k∈z时,h(x)取得最小值为 1-
.
方案②若把f(x)的图象向下平移
个单位,得到g(x)=sinx-
,
∴h(x)=sinx(sinx-
)=(sinx-
)2-
,
∴当sinx=1时,即 x=2kπ+
,k∈z时,h(x)取得最小值为 1-
.
方案③若把f(x)的图象向左平移
个单位,得到g(x)=sin(x+
),
∴h(x)=sinx•sin(x+
)=sinx(-
sinx+
cosx)=-
+
sin2x=
sin(2x+
)-
,
∴当2x+
=2kπ-
,即 x=kπ-
,k∈z时,h(x)取得最小值为-
.
方案④若把f(x)的图象向右平移
个单位,得到g(x)=sin(x-
),
∴h(x)=sinx•sin(x-
)=sinx(-
sinx-
cosx)=-
-
sin2x=
sin(2x-
)-
,
∴当2x-
=2kπ-
,即 x=kπ+
,k∈z时,h(x)取得最小值为-
.
| a |
| b |
| x |
| 2 |
| x |
| 2 |
| π |
| 2 |
| π |
| 2 |
(Ⅱ)方案①若把f(x)的图象向上平移
| 2π |
| 3 |
| 2π |
| 3 |
∴h(x)=sinx(sinx+
| 2π |
| 3 |
| π |
| 3 |
| π2 |
| 9 |
∴当sinx=-1,即 x=2kπ-
| π |
| 2 |
| 2π |
| 3 |
方案②若把f(x)的图象向下平移
| 2π |
| 3 |
| 2π |
| 3 |
∴h(x)=sinx(sinx-
| 2π |
| 3 |
| π |
| 3 |
| π2 |
| 9 |
∴当sinx=1时,即 x=2kπ+
| π |
| 2 |
| 2π |
| 3 |
方案③若把f(x)的图象向左平移
| 2π |
| 3 |
| 2π |
| 3 |
∴h(x)=sinx•sin(x+
| 2π |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 1-cos2x |
| 4 |
| ||
| 4 |
| 1 |
| 2 |
| π |
| 6 |
| 1 |
| 4 |
∴当2x+
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
| 3 |
| 4 |
方案④若把f(x)的图象向右平移
| 2π |
| 3 |
| 2π |
| 3 |
∴h(x)=sinx•sin(x-
| 2π |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 1-cos2x |
| 4 |
| ||
| 4 |
| 1 |
| 2 |
| π |
| 6 |
| 1 |
| 4 |
∴当2x-
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
| 3 |
| 4 |
点评:本题主要考查两个向量的数量积公式、正弦函数的增区间、函数y=Asin(ωx+φ)的图象变换规律,体现了分类讨论的数学思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
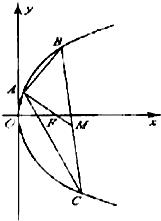 已知点A(2,8),B(x1,y1),C(x2,y2)在抛物线y2=2px,(p>0)上,△ABC的重心与此抛物线的焦点F重合(如图)
已知点A(2,8),B(x1,y1),C(x2,y2)在抛物线y2=2px,(p>0)上,△ABC的重心与此抛物线的焦点F重合(如图)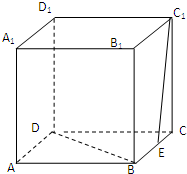 在正方体ABCD-A1B1C1D1中,E为BC的中点,求:
在正方体ABCD-A1B1C1D1中,E为BC的中点,求: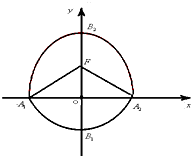 如图,曲线C由半椭圆
如图,曲线C由半椭圆 如图,在正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,P是DD1的中点,设Q是CC1上的中点,求证:PO∥面D1BQ.
如图,在正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,P是DD1的中点,设Q是CC1上的中点,求证:PO∥面D1BQ.