题目内容

由正方体的八个顶点中的任意两个所确定的所有直线中取出两条，这两条直线是异面直线的概率是
 
．
考点：古典概型及其概率计算公式
专题：概率与统计
分析：因为从正方体的八个顶点中任取两个点共有C82条直线，从中任意取出两条有C282种取法，从八个顶点任取四个不共面的点共有C84-12组；而其中每一组不共面的四点可出现3对异面直线．得到概率．
解答： 解：因为从正方体的八个顶点中任取两个点共有C82=28条直线，
从中任意取出两条有C282种取法，
从八个顶点任取四个不共面的点共有C84-12组；
而其中每一组不共面的四点可出现3对异面直线．
∴所求的概率为P=
C
4
8
-12
C
2
8
=
29
63
．
故答案为：
29
63
．
点评：本题主要考查异面直线及其判断、等可能事件的概率等基础知识，本题解题的关键是看出符合条件的异面直线的条数，是基础题．
练习册系列答案
相关题目
已知
a
=（2cos
x
2
，1），
b
=（sin
x
2
，0），f（x）=
a
•
b
．
（Ⅰ）求函数f（x）的单调递增区间；
（Ⅱ）若将f（x）的图象平移
2π
3
个单位（可向上、下、左、右平移，且仅可选择一种方向平移一次）得到g（x），求h（x）=f（x）g（x）的最小值．
已知函数f（x）=ax2+（1-2a）x-lnx（a∈R）．
（1）当a＞0时，求函数f（x）的单调增区间；
（2）当a＜0时，求函数f（x）在区间[
1
2
，1]上的最小值．
已知圆O：x2+y2=4和圆C：x2+（y-4）2=1．
（Ⅰ）判断圆O和圆C的位置关系；
（Ⅱ）过圆C的圆心C作圆O的切线l，求切线l的方程；
（Ⅲ）过圆C的圆心C作动直线m交圆O于A，B两点．试问：在以AB为直径的所有圆中，是否存在这样的圆P，使得圆P经过点M（2，0）？若存在，求出圆P的方程；若不存在，请说明理由．
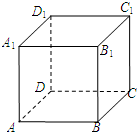在如图所示的正方体ABCD-A1B1C1D1中，E、F分别为棱AB与AA1的中点，则直线EF与平面ACC1A1成角的大小为
 
．
直线a在平面α外，是指直线a和平面α
 
或
 
．
曲线
x2
25λ
-
y2
16λ
=1（λ≠0）的渐近线方程为
 
．
一个非空集合中的各个元素之和是3的倍数，则称该集合为“好集”．记集合{1，2，3，…，3n}的子集中所有“好集”的个数为f（n）．
（1）求f（1），f（2）的值；
（2）求f（n）的表达式．
不等式|x-3|＜x-1的解集是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网