题目内容

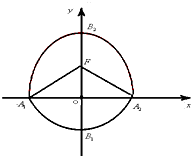如图，曲线C由半椭圆
y2
a2
+
x2
b2
=1（y≥0）与圆弧x2+（y-c）2=a2（y≤0）组成的，F（0，c）为半椭圆的一个焦点，A1、A2和B1、B2分别是曲线C与x轴、y轴交点，已知椭圆的离心率e=
1
2
，S △FA1B1=
3
．
（Ⅰ）求a，b，c的值；
（Ⅱ）过点F且不与x轴垂直的直线l交曲线C于P、Q两点．
（i）求证：当且仅当P，Q均在半椭圆
y2
a2
+
x2
b2
=1（y≥0）上时，△B1PQ的周长L取最大，且最大值为8；
（ii）当△B1PQ的周长L取最大时，求弦PQ长度的取值范围．
考点：直线与圆锥曲线的综合问题
专题：圆锥曲线中的最值与范围问题
分析：（Ⅰ）由已知条件推导出
c
a
=
1
2
1
2
•2b•c=
3
a2=b2+c2
，由此能求出结果．
（Ⅱ）（i）设直线l的斜率为k．当-
3
3
≤k≤
3
3
时，P，Q均在椭圆
x2
4
+
y2
3
=1，x≥0上，△B1PQ的周长L=|B1Q|+|FQ|+|FP|+|B1P|=4a=8；当k＜-
3
3
或k＞
3
3
时，P，Q其一在椭圆
x2
4
+
y2
3
=1（x≥0）上，另一在圆弧x2+（y-c）2=a2（y≤0）上，由此求出△B1PQ的周长L=|B1Q|+|FQ|+|FP|+|B1P|＜8，从而得到证明．
（ii）解：由（i）知△B1PQ的周长L取最大时-
3
3
≤k≤
3
3
．设PQ的方程为y=kx+1（-
3
3
≤k≤
3
3
），P（x1，y1），Q（x2，y2），由
y=kx+1
y2
4
+
x2
3
=1
，得（4+3k2）x2+6kx-9=0，由此能求出弦PQ长度的取值范围是[3，
16
5
]．
解答： （Ⅰ）解：依题意得
c
a
=
1
2
1
2
•2b•c=
3
a2=b2+c2
，
解得a=2，b=
3
，c=1．
（Ⅱ）（i）证明：设直线l的斜率为k．
当-
3
3
≤k≤
3
3
时，P，Q均在椭圆
x2
4
+
y2
3
=1，x≥0上，
∴△B1PQ的周长L=|B1Q|+|FQ|+|FP|+|B1P|=4a=8，（6分）
当k＜-
3
3
或k＞
3
3
时，P，Q其一在椭圆
x2
4
+
y2
3
=1（x≥0）上，
另一在圆弧x2+（y-c）2=a2（y≤0）上，设直线l的倾斜角为α．
若k＞
3
3
，则30°＜α＜90°，
∴△B1PQ的周长
L=|B1Q|+|FQ|+|FP|+|B1P|
=2a+r+2rsin（45°-
α
2
）=6+4sin（45°-
α
2
），
∵0°＜45°-
α
2
＜30°，∴0＜sin（45°-
α
2
）＜
1
2
，
∴L=6+4sin（45°-
α
2
）＜8，（8分）
若k＜-
3
3
时，则90°＜α＜150°，
∴△B1PQ的周长
L=|B1Q|+|FQ|+|FP|+|B1P|
=2a+r+2rsin（
α
2
-45°）=6+4sin（
α
2
-45°），
∵0°＜
α
2
-45°＜30°，∴0＜sin（
α
2
-45°）＜
1
2
，
∴L=6+4sin（
α
2
-45°）＜8，．
∴当且仅当P，Q均在椭圆
x2
4
+
y2
3
=1，x≥0上时，△B1PQ的周长L取最大，
且最大值为8．（9分）
（ii）解：由（i）知：当且仅当P，Q均在椭圆
x2
4
+
y2
3
=1，x≥0上时，
△B1PQ的周长L取最大，且最大值为8．此时-
3
3
≤k≤
3
3
．
设PQ的方程为y=kx+1（-
3
3
≤k≤
3
3
），P（x1，y1），Q（x2，y2），
由
y=kx+1
y2
4
+
x2
3
=1
，得（4+3k2）x2+6kx-9=0，
△＞0，x1+x2=-
6k
4+3k2
，x1x2=
-9
4+3k2
，（11分）
∴|PQ|=
(x1-x2)2+(y1-y2)2
=
(1+k2)(x1-x2)2

=
(1+k2)[(x1+x2)2-4x1x2]

=
(1+k2)[
36k2
(4+3k2)2
+
36
4+3k2
]

=
36•4(k2+1)2
(4+3k2)2
=
12(k2+1)
4+3k2
=4（1-
1
4+3k2
），
∵k2∈[0，
1
3
]，∴|PQ|∈[3，
16
5
]，∴弦PQ长度的取值范围是[3，
16
5
]．（14分）
点评：本题考查椭圆中参数的求法，考查三角形周长的最大值满足的条件的证明，考查弦长的取值范围的求法，解题时要认真审题，注意椭圆弦长公式的合理运用．
练习册系列答案
相关题目
已知二阶矩阵M=
2  1
0  1
，求矩阵M特征值及特征向量．
如图，三棱柱ABC-A1B1C1中，AA1⊥平面ABC，∠ACB=90°，AC=BC=1，AA1=2．以AB，BC为邻边作平行四边形ABCD，连接DA1和DC1．
（Ⅰ）求证：A1D∥平面BCC1B1；
（Ⅱ）求直线CC1与平面DA1C1所成角的正弦值．
已知函数f（x）=x2，g（x）=ax-lnx，
（Ⅰ）若函数f（x）+g（x）在[2，3]上是减函数，求实数a的取值范围；
（Ⅱ）是否存在实数a，当x∈（0，e]（e是自然常数）时，函数g（x）的最小值是3，若存在，求出a的值；若不存在，说明理由；
（Ⅲ）当x∈（0，e]时，证明：e2x＞
5
2
+（1+
1
x
）lnx．
已知圆O：x2+y2=4．
（1）直线l1：
3
x+y-2
3
=0与圆O相交于A、B两点，求|AB|；
（2）如图，设M（x1，y1）、P（x2，y2）是圆O上的两个动点，点M关于原点的对称点为M1，点M关于x轴的对称点为M2，如果直线PM1、PM2与y轴分别交于（0，m）和（0，n），问m•n是否为定值？若是求出该定值；若不是，请说明理由；
（3）过O点任作一直线与直线x=4交于E点，过（2，0）点作直线与OE垂直，并且交直线x=4于F点，以EF为直径的圆是否过定点，如过定点求出其坐标，如不过，请说明理由．
已知
a
=（2cos
x
2
，1），
b
=（sin
x
2
，0），f（x）=
a
•
b
．
（Ⅰ）求函数f（x）的单调递增区间；
（Ⅱ）若将f（x）的图象平移
2π
3
个单位（可向上、下、左、右平移，且仅可选择一种方向平移一次）得到g（x），求h（x）=f（x）g（x）的最小值．
如图，离心率为
2
2
的椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）与直线l：x=-2相切于点A（-2，0）．
（Ⅰ）求椭圆的方程；
（Ⅱ）若OA是圆C的直径，P（x0，y0）（x0＞0）为椭圆上的动点，过P作圆C的两条切线，分别交直线l于点M、N，求当
PM
•
PN
取得最小值时P点的横坐标x0．
已知直线y=kx与圆N：x2+y2-2x-2y+1=0交于P、Q，且M（0，b），
MP
•
MQ
=0，问是否存在k使得M，N，P，Q4点共圆？若存在，求出k值；若不存在，说明理由．
在如图所示的正方体ABCD-A1B1C1D1中，E、F分别为棱AB与AA1的中点，则直线EF与平面ACC1A1成角的大小为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网