题目内容
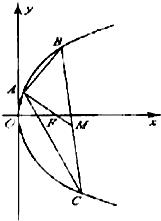 已知点A(2,8),B(x1,y1),C(x2,y2)在抛物线y2=2px,(p>0)上,△ABC的重心与此抛物线的焦点F重合(如图)
已知点A(2,8),B(x1,y1),C(x2,y2)在抛物线y2=2px,(p>0)上,△ABC的重心与此抛物线的焦点F重合(如图)(1)写出该抛物线的方程和焦点F的坐标;
(2)求线段BC中点M的坐标;
(3)求BC所在直线的方程.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由点A(2,8)在抛物线y2=2px,(p>0)上,利用待定系数法能求出抛物线方程.
(2)由已知条件知F(8,0)是线段AM的定比分点,且
=2,由此能求出点M的坐标.
(3)设BC的直线为:y+4=k(x-11),(k≠0),由
,得ky2-32y-32(11k+4)=0,由此能求出BC所在的直线方程.
(2)由已知条件知F(8,0)是线段AM的定比分点,且
| AF |
| FM |
(3)设BC的直线为:y+4=k(x-11),(k≠0),由
|
解答:
解:(1)∵点A(2,8)在抛物线y2=2px,(p>0)上,
∴64=4p,解得p=16,
∴抛物线方程为y2=32x,焦点F的坐标为F(8,0).
(2)如图,∵F(8,0)是△ABC的重心,M是BC中点,
∴F是线段AM的定比分点,且
=2,
设点M的坐标为(x2,y2),
则
=8,
=0,
解得x2=11,y2=-4,
∴点M的坐标为M(11,-4).
(3)∵线段BC的中点M不在x轴上,
∴BC所在的直线不垂直于x轴,设BC的直线为:y+4=k(x-11),(k≠0),
由
,得ky2-32y-32(11k+4)=0,
∴y1+y2=
,
由(2)的结论得
=-4,解得k=-4.
∴BC所在的直线方程为4x+y-40=0.
∴64=4p,解得p=16,
∴抛物线方程为y2=32x,焦点F的坐标为F(8,0).
(2)如图,∵F(8,0)是△ABC的重心,M是BC中点,
∴F是线段AM的定比分点,且
| AF |
| FM |
设点M的坐标为(x2,y2),
则
| 2+2x2 |
| 1+2 |
| 8+2y2 |
| 1+2 |
解得x2=11,y2=-4,
∴点M的坐标为M(11,-4).
(3)∵线段BC的中点M不在x轴上,
∴BC所在的直线不垂直于x轴,设BC的直线为:y+4=k(x-11),(k≠0),
由
|
∴y1+y2=
| 32 |
| k |
由(2)的结论得
| y1+y2 |
| 2 |
∴BC所在的直线方程为4x+y-40=0.
点评:本题考查抛物线方程的求法,考查线段中点坐标的求不法,考查直线方程的求法,解题时要认真审题,注意定比分点公式的合理运用.

练习册系列答案
相关题目
直线l过点A(2,4)且与圆x2+y2=4相切,则l的方程是( )
| A、3x-4y+10=0 |
| B、x=2或3x-4y+10=0 |
| C、x-y+2=0 |
| D、x=2或x-y+2=0 |
 已知:如图AD,BC,AE分别是⊙O的三条切线,切点分别是D,E,F,AG是⊙O的一条割线,交⊙O于F,G两点,△ABC的周长2
已知:如图AD,BC,AE分别是⊙O的三条切线,切点分别是D,E,F,AG是⊙O的一条割线,交⊙O于F,G两点,△ABC的周长2 如图,四棱锥A-BCDE,平面ABC⊥平面BCDE,△ABC边长为2的等边三角形,底面BCDE是矩形,且CD=
如图,四棱锥A-BCDE,平面ABC⊥平面BCDE,△ABC边长为2的等边三角形,底面BCDE是矩形,且CD=