题目内容
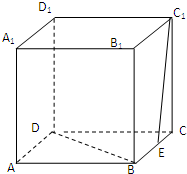在正方体ABCD-A1B1C1D1中，E为BC的中点，求：（1）求异面直线C1E与BD 所成角的余弦值；
（2）求二面角C1-DE-C的余弦值．
考点：二面角的平面角及求法,异面直线及其所成的角
专题：综合题,空间位置关系与距离,空间角
分析：（1）取CD中点为F，连接EF，证明∠FEC1为异面直线C1E与BD所成角，通过解三角形求出△FEC1的三边长，然后利用余弦定理求角的余弦值；
（2）过C作CH⊥DE于H，连接C1H，则∠C1HC就是二面角C1-DE-C的平面角，求出CH，C1H，即可求二面角C1-DE-C的余弦值．
（2）过C作CH⊥DE于H，连接C1H，则∠C1HC就是二面角C1-DE-C的平面角，求出CH，C1H，即可求二面角C1-DE-C的余弦值．
解答：
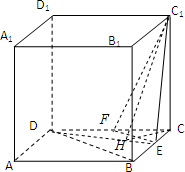解：（1）设正方体边长为2，取CD中点为F，连接EF，则EF∥BD，EF=
，C1E=
，
∴∠FEC1为异面直线C1E与BD所成角，
∴cos∠FEC1=
=
；
（2）过C作CH⊥DE于H，连接C1H，则∠C1HC就是二面角C1-DE-C的平面角，
∵CD=2，CE=1，
∴DE=
，
∴CH=
，
∵CC1=2，∴C1H=
∴cos∠C1HC=
．
解：（1）设正方体边长为2，取CD中点为F，连接EF，则EF∥BD，EF=| 2 |
| 5 |
∴∠FEC1为异面直线C1E与BD所成角，
∴cos∠FEC1=
| 2+5-5 | ||||
2
|
| ||
| 10 |
（2）过C作CH⊥DE于H，连接C1H，则∠C1HC就是二面角C1-DE-C的平面角，
∵CD=2，CE=1，
∴DE=
| 5 |
∴CH=
2
| ||
| 5 |
∵CC1=2，∴C1H=
|
∴cos∠C1HC=
| ||
| 6 |
点评：本题考查了异面直线所成的角的求法，二面角的平面角，训练了利用余弦定理求角，是中档题，正确作出二面角的平面角是关键．
练习册系列答案
精英口算卡系列答案
应用题点拨系列答案
相关题目
已知：如图AD，BC，AE分别是⊙O的三条切线，切点分别是D，E，F，AG是⊙O的一条割线，交⊙O于F，G两点，△ABC的周长2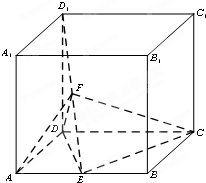
如图，四棱柱ABCD-A1B1C1D1中，DD1⊥底面ABCD．ABCD为平行四边形，∠DAB=60°，AB=2AD=2．DD1=3，E，F分别是AB与D1E的中点．