题目内容
设x,y,z都是正实数,a=x+
,b=y+
,c=z+
.
求证:a,b,c三数中至少有一个不小于2
.
| 2 |
| y |
| 2 |
| z |
| 2 |
| x |
求证:a,b,c三数中至少有一个不小于2
| 2 |
考点:反证法与放缩法,不等式的证明
专题:证明题,反证法
分析:根据用反证法证明数学命题的方法和步骤,可得结论.
解答:
证明:假设a,b,c三数都小于2
,则a+b+c<2
∵x,y,z都是正实数,
∴a+b+c=x+
+y+
+z+
≥2
+2
+2
=6
,
与a+b+c<2
矛盾.
∴a,b,c三数中至少有一个不小于2
.
| 2 |
| 2 |
∵x,y,z都是正实数,
∴a+b+c=x+
| 2 |
| y |
| 2 |
| z |
| 2 |
| x |
| 2 |
| 2 |
| 2 |
| 2 |
与a+b+c<2
| 2 |
∴a,b,c三数中至少有一个不小于2
| 2 |
点评:本题主要考查用反证法证明数学命题的方法和步骤,属于中档题.

练习册系列答案
相关题目
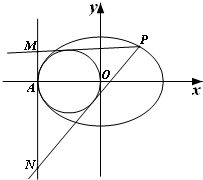 如图,离心率为
如图,离心率为