题目内容
20．设函数f（x）=$\left\{\begin{array}{l}{（x-a）^2}+e，x≤2\\ \frac{x}{1nx}+a+10，x＞2\end{array}$，（e是自然对数的底数），若f（2）是函数f（x）的最小值，则a的取值范围是（ ）| A． | [-1，6] | B． | [1，4] | C． | [2，4] | D． | [2，6] |
分析 x≤2时，函数的对称轴为x=a，可确定a≥2，再利用f（e）是函数的极小值，f（e）≥f（2），即可求出a 的范围．
解答 解：x≤2时，函数的对称轴为x=a，∵f（2）是函数f（x）的最小值，∴a≥2．
x＞2，f（x）=$\frac{x}{lnx}$+a+10，f′（x）=$\frac{lnx-1}{l{n}^{2}x}$，x∈（2，e），f′（x）＜0，x∈（2，+∞），f′（x）＞0，∴f（e）是函数的极小值，
∵f（2）是函数f（x）的最小值，
∴f（e）≥f（2），∴1≤a≤6，
∴1≤a≤6．
故选：D．
点评 本题考查函数的最值，考查导数知识的综合运用，确定函数的单调性是关键．
练习册系列答案
相关题目
10．
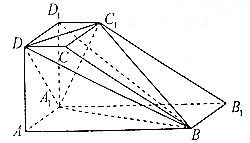如图，直四棱柱ABCD-A1B1C1D1的底面ABCD是直角梯形，其中AB⊥AD，AB=2AD=2AA1=4，CD=1．
（Ⅰ）证明：BD1⊥平面A1C1D；
（Ⅱ）求多面体BDC1A1D1的体积．
如图，直四棱柱ABCD-A1B1C1D1的底面ABCD是直角梯形，其中AB⊥AD，AB=2AD=2AA1=4，CD=1．（Ⅰ）证明：BD1⊥平面A1C1D；
（Ⅱ）求多面体BDC1A1D1的体积．
11．已知F1、F2为双曲线的焦点，过F2垂直于实轴的直线交双曲线于A、B两点，BF1交y轴于点C，若AC⊥BF1，则双曲线的离心率为（ ）
| A． | $\sqrt{2}$ | B． | $\sqrt{3}$ | C． | 2$\sqrt{2}$ | D． | 2$\sqrt{3}$ |
15．若集合P={x∈R|x＞0}，Q={x∈Z|（x+1）（x-4）＜0}，则P∩Q=（ ）
| A． | （0，4） | B． | （4，+∞） | C． | {1，2，3} | D． | {1，2，3，4} |
5．一企业从某条生产线上随机抽取100件产品，测量这些产品的某项技术指标值x，得到如下的频率分布表：
（Ⅰ）作出样本的频率分布直方图，并估计该技术指标值x的平均数和众数；
（Ⅱ）若x＜13或x≥21，则该产品不合格．现从不合格的产品中随机抽取2件，求抽取的2件产品中技术指标值小于13的产品恰有一件的概率．
| x | [11，13） | [13，15） | [15，17） | [17，19） | [19，21） | [21，23） |
| 频数 | 2 | 12 | 34 | 38 | 10 | 4 |
（Ⅱ）若x＜13或x≥21，则该产品不合格．现从不合格的产品中随机抽取2件，求抽取的2件产品中技术指标值小于13的产品恰有一件的概率．