题目内容
8.抛物线y2=8x的焦点到双曲线${x^2}-\frac{y^2}{3}=1$的渐近线的距离是$\sqrt{3}$.分析 求出抛物线y2=8x的焦点坐标、双曲线${x^2}-\frac{y^2}{3}=1$的渐近线,即可求出结论.
解答 解:抛物线y2=8x的焦点(2,0)到双曲线${x^2}-\frac{y^2}{3}=1$的渐近线y=$±\sqrt{3}$x的距离是d=$\frac{|±2\sqrt{3}|}{\sqrt{3+1}}$=$\sqrt{3}$,
故答案为$\sqrt{3}$.
点评 本题考查抛物线、双曲线的性质,考查点到直线距离公式的运用,属于中档题.

练习册系列答案
相关题目
3.已知集合M={x|x2=x},N={-1,0,1},则M∩N=( )
| A. | {-1,0,1} | B. | {0,1} | C. | {1} | D. | {0} |
 在△ABC中,角A、B、C所对的边分别是a、b、c,已知$\sqrt{3}a=2csinA$且c<b.
在△ABC中,角A、B、C所对的边分别是a、b、c,已知$\sqrt{3}a=2csinA$且c<b. 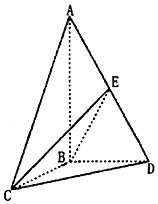 如图,三棱锥A-BCD中,AB⊥平面BCD,AC=AD=2,BC=BD=1,点E是线段AD的中点.
如图,三棱锥A-BCD中,AB⊥平面BCD,AC=AD=2,BC=BD=1,点E是线段AD的中点.